Quảng cáo
Trả lời:
Câu hỏi cùng đoạn
Câu 3:
không nghịch biến trên
Phương án C, Ta có: . Nên \({y^'} = 0 \Leftrightarrow x = 0\) và \({y^'}\) đổi dấu khi đi qua \(x = 0\). Suy ra hàm số không nghịch biến trên \(\mathbb{R}\).
Phương án A, Hàm số: .
\({\Delta ^'} = - 6053 < 0\) nên \({y^'} < 0,\forall x \in \mathbb{R}\) và hàm số nghịch biến trên \(\mathbb{R}\).
Phương án B, Hàm số: \(y = - 5x + \sin x \Rightarrow {y^'} = - 5 + \cos x < 0,\forall x \in \mathbb{R}\). Nên hàm số nghịch biến trên \(\mathbb{R}\).
Phương án D, Hàm số: \(y = {\left( {\frac{\pi }{{\sqrt 3 + \sqrt 5 }}} \right)^x} \Rightarrow {y^'} = {\left( {\frac{\pi }{{\sqrt 3 + \sqrt 5 }}} \right)^x}\ln \frac{\pi }{{\sqrt 3 + \sqrt 5 }} < 0,\forall x \in \mathbb{R}\). Nên hàm số nghịch biến trên \(\mathbb{R}\). Chọn Đ
Câu 4:
\(y = {\left( {\frac{\pi }{{\sqrt 3 + \sqrt 5 }}} \right)^x}\)không nghịch biến trên R.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
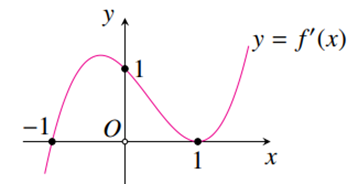
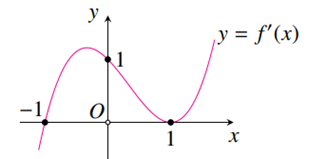
Dựa đồ thị hàm số \(y = f'\left( x \right)\) ta thấy \(y = f'\left( x \right)\) là hàm số xác định và liên tục trên \(\mathbb{R}\), \(f'\left( x \right) < 0,\;\forall x \in \left( { - \infty \;;\; - 1} \right)\), \(f'\left( x \right) \ge 0,\;\forall x \in \left( { - 1\;;\; + \infty } \right)\) nên hàm số \(y = f\left( x \right)\) có điểm cực tiểu là \(x = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.