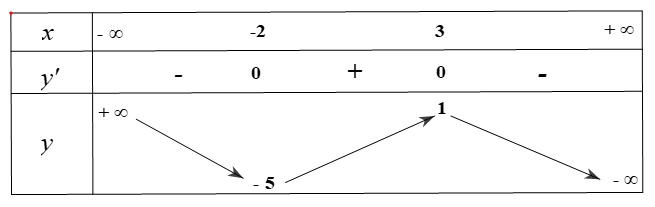
Các mệnh đề sau đúng hay sai.
Cực đại của hàm số \(y = x\sqrt {1 - {x^2}} \) là \(\frac{1}{2}\)
Quảng cáo
Trả lời:
Tập xác định là \(\left[ { - 1;\,1} \right]\)
Ta có \(y' = \sqrt {1 - {x^2}} + x\frac{{ - x}}{{\sqrt {1 - {x^2}} }} = \frac{{1 - 2{x^2}}}{{\sqrt {1 - {x^2}} }}\)
\(y' = 0 \Leftrightarrow x = \pm \frac{{\sqrt 2 }}{2}\)
Bảng biến thiên
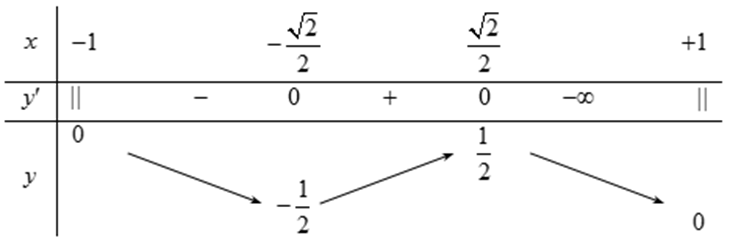
Ta thấy cực đại của hàm số là \(\frac{1}{2}\).
Câu hỏi cùng đoạn
Câu 2:
Điểm thuộc đường thẳng \(d:\)\(x - y - 1 = 0\) cách đều hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) là \(I\left( {1; - 1} \right)\)
Ta có: \(y' = 3{x^2} - 6x\).
Cho \(y' = 0\)\[ \Leftrightarrow 3{x^2} - 6x = 0\]\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 2\\x = 2 \Rightarrow y = - 2\end{array} \right.\).
Hai điểm cực trị của đồ thị hàm số là \(A\left( {0;2} \right)\), \(B\left( {2; - 2} \right)\).
Gọi \(I\left( {{x_I};{x_I} - 1} \right) \in d\). Ta có: \(IA = IB\)\( \Leftrightarrow I{A^2} = I{B^2}\)\( \Leftrightarrow {x_I}^2 + {\left( {3 - {x_I}} \right)^2} = {\left( {2 - {x_I}} \right)^2} + {\left( { - {x_I} - 1} \right)^2}\)
\( \Leftrightarrow {x_I}^2 + 9 - 6{x_I} + {x_I}^2 = 4 - 4{x_I} + {x_I}^2 + {x_I}^2 + 2{x_I} + 1\)\( \Leftrightarrow 4{x_I} = 4\)\( \Leftrightarrow {x_I} = 1\).
\( \Rightarrow I\left( {1;0} \right)\).
Câu 3:
Biết \[M\left( {-{\rm{ }}2;21} \right)\] là điểm cực đại của đồ thị hàm số \(y = 2{x^3} + b{x^2} + cx + 1\). Điểm cực tiểu của đồ thị hàm số đã cho là \(\left( {1; - 6} \right)\)
Ta có: \(y' = 6{x^2} + 2bx + c\). Vì \[M\left( {--{\rm{ }}2;21} \right)\] là điểm cực đại của đồ thị nên
\(\left\{ \begin{array}{l}y'\left( { - 2} \right) = 0\\y\left( { - 2} \right) = 21\end{array} \right. \Rightarrow \left\{ \begin{array}{l} - 4b + c = - 24\\4b - 2c = 36\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\c = - 12\end{array} \right.\) \( \Rightarrow y' = 6{x^2} + 6x - 12\).
\(y' = 0 \Leftrightarrow 6{x^2} + 6x - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\).
Ta có: \(y\left( 1 \right) = 2 + 3 - 12 + 1 = - 6\) suy ra điểm cực tiểu của đồ thị hàm số là \(\left( {1; - 6} \right)\).
Câu 4:
Gọi\(A,\,B,\,C\) là ba điểm cực trị của đồ thị hàm số \(y = {x^4} - 2{x^2} + 2\). Diện tích của tam giác \(ABC\) bằng 2.
TXĐ: \(D = R.\)
Ta có: \(y' = 4{x^3} - 4x\)
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = - 1}\\{x = 1}\end{array}} \right.\)

Từ hình vẽ, suy ra \({S_{\Delta ABC}} = 2{S_{\Delta AHC}} = 2.\frac{1}{2}.AH.HC = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
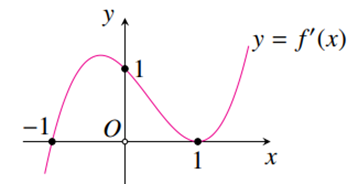
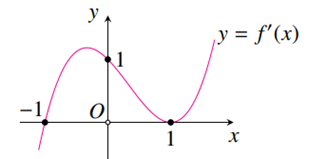
Dựa đồ thị hàm số \(y = f'\left( x \right)\) ta thấy \(y = f'\left( x \right)\) là hàm số xác định và liên tục trên \(\mathbb{R}\), \(f'\left( x \right) < 0,\;\forall x \in \left( { - \infty \;;\; - 1} \right)\), \(f'\left( x \right) \ge 0,\;\forall x \in \left( { - 1\;;\; + \infty } \right)\) nên hàm số \(y = f\left( x \right)\) có điểm cực tiểu là \(x = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.