Tìm chu vi và diện tích hình tròn có:
\(r = 5{\rm{cm}}\); \(r = 0,8{\rm{cm}}\); \(r = \frac{4}{5}{\rm{dm}}\).
Tìm chu vi và diện tích hình tròn có:
\(r = 5{\rm{cm}}\); \(r = 0,8{\rm{cm}}\); \(r = \frac{4}{5}{\rm{dm}}\).
Câu hỏi trong đề: 15 bài tập Hình tròn có lời giải !!
Quảng cáo
Trả lời:
Hướng Dẫn Giải
- \(r = 5{\rm{cm}}:C = 2 \times 5 \times 3,14 = 31,4{\rm{ cm}};S = 5 \times 5 \times 3,14 = 78,5{\rm{c}}{{\rm{m}}^2}\)
- \(r = 0,8{\rm{cm}}:C = 2 \times 0,8 \times 3,14 = 5,024{\rm{ cm}};S = 0,8 \times 0,8 \times 3,14 = 2,0096{\rm{c}}{{\rm{m}}^2}\)
- \(r = \frac{4}{5}{\rm{dm}}:C = 2 \times \frac{4}{5} \times 3,14 = 5,024{\rm{dm}};S = \frac{4}{5} \times \frac{4}{5} \times 3,14 = 2,0096{\rm{ d}}{{\rm{m}}^2}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng Dẫn Giải
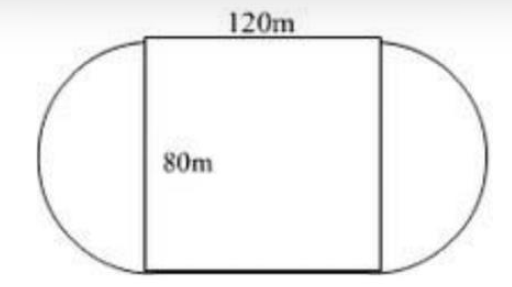
Nhận xét: Sân vận động gồm hai nửa hình tròn đường kính 80m và hình chữ nhật có chiều dài 120m, chiều rộng 80m.
a) Chu vi hai nửa đường tròn là: \(80 \times 3,14 = 251,2\) (m)
Chu vi sân vận động là: \(251,2 + 120 \times 2 = 491,2\) (m)
b) Bán kính mỗi nửa đường tròn là: \(80:2 = 40\) (m)
Diện tích hai nửa đường tròn là: \(40 \times 40 \times 3,14 = 5024\) (\({m^2}\))
Diện tích phần hình chữ nhật là: \(80 \times 120 = 9600\) (\({m^2}\))
Diện tích sân vận động là: \(5024 + 9600 = 14624\) (\({m^2}\))
Đáp Số: a) 491,2m b) 14624 (\({m^2}\))
Lời giải
Hướng Dẫn Giải
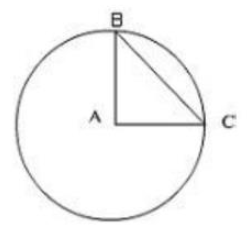
Bán kính hình tròn tâm A là: \(37,68:3,14:2 = 6\) (cm)
Thấy AB = AC và bằng bán kính hình tròn tâm O. Do đó:
Diện tích tam giác ABC là: \(\frac{1}{2} \times 6 \times 6 = 18\) (\(c{m^2}\))
Đáp Số: 18 \(c{m^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.