Cho tam giác \(ABC\) có \(\cos A = \frac{1}{3}\), \(BC = 9\) và \(AC = 6\), \(M\) là trung điểm cạnh \(BC\).
a) Độ dài cạnh \(AB = 8\).
b) Diện tích hình tròn ngoại tiếp tam giác \(ABC\) là \({S_{{\rm{ht1}}}} = 9\pi \).
c) Giá trị \(\cos \widehat {AMB}\) bằng \(\frac{{\sqrt 3 }}{5}\).
d) Tính diện tích của hình tròn nội tiếp tam giác \(ABC\) là \({S_{{\rm{ht2}}}} = \pi {r^2} = \frac{{9\pi }}{2}\).
Cho tam giác \(ABC\) có \(\cos A = \frac{1}{3}\), \(BC = 9\) và \(AC = 6\), \(M\) là trung điểm cạnh \(BC\).
a) Độ dài cạnh \(AB = 8\).
b) Diện tích hình tròn ngoại tiếp tam giác \(ABC\) là \({S_{{\rm{ht1}}}} = 9\pi \).
c) Giá trị \(\cos \widehat {AMB}\) bằng \(\frac{{\sqrt 3 }}{5}\).
d) Tính diện tích của hình tròn nội tiếp tam giác \(ABC\) là \({S_{{\rm{ht2}}}} = \pi {r^2} = \frac{{9\pi }}{2}\).
Quảng cáo
Trả lời:
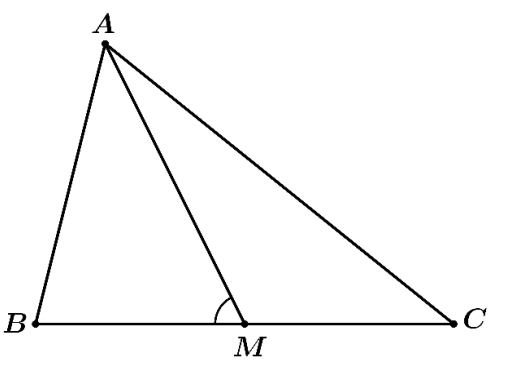
a) Sai. Áp dụng định lí côsin trong tam giác \(ABC\), ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A\)\( \Leftrightarrow {9^2} = A{B^2} + {6^2} - 2 \cdot AB \cdot 6 \cdot \frac{1}{3}\)
\( \Leftrightarrow A{B^2} - 4AB - 45 = 0 \Rightarrow AB = 9\) (vì \(AB > 0\)).
b) Sai. Ta có \(\cos A = \frac{1}{3}\)\( \Rightarrow \sin A = \frac{{2\sqrt 2 }}{3}\).
Từ định lí sin, ta suy ra bán kính đường tròn ngoại tiếp tam giác \(ABC\) là:
\(R = \frac{{BC}}{{2\sin A}} = \frac{9}{{2 \cdot \frac{{2\sqrt 2 }}{3}}} = \frac{{27}}{{4\sqrt 2 }}\). Vậy \({S_{ht1}} = \pi {R^2} = \pi \cdot {\left( {\frac{{27}}{{4\sqrt 2 }}} \right)^2} = \frac{{729\pi }}{{32}}\).
c) Sai. Ta có \(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB \cdot BC}} = \frac{{{9^2} + {9^2} - {6^2}}}{{2 \cdot 9 \cdot 9}} = \frac{7}{9}\); \(MB = MC = \frac{{BC}}{2} = \frac{9}{2}\).
Khi đó, \(A{M^2} = A{B^2} + M{B^2} - 2AB \cdot MB \cdot \cos B = {9^2} + {\left( {\frac{9}{2}} \right)^2} - 2 \cdot 9 \cdot \frac{9}{2} \cdot \frac{7}{9} = \frac{{153}}{4}\).
Suy ra \(AM = \frac{{\sqrt {153} }}{2}\).
Vậy \(\cos \widehat {AMB} = \frac{{A{M^2} + M{B^2} - A{B^2}}}{{2AM \cdot MB}} = \frac{{\frac{{153}}{4} + {{\left( {\frac{9}{2}} \right)}^2} - {9^2}}}{{2 \cdot \frac{{\sqrt {153} }}{2} \cdot \frac{9}{2}}} = - \frac{{5\sqrt {17} }}{{51}}\).
d) Đúng. Nửa chu vi của tam giác \(ABC\) là \(p = \frac{{AB + AC + BC}}{2} = 12\).
Diện tích của tam giác \(ABC\) là \(S = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} = 18\sqrt 2 \).
Với \(r\) là bán kính đường tròn nội tiếp tam giác \(ABC\), ta có \(S = pr\).
Suy ra \(r = \frac{S}{p} = \frac{{18\sqrt 2 }}{{12}} = \frac{{3\sqrt 2 }}{2}\). Vậy \({S_{ht2}} = \pi {r^2} = \pi \cdot {\left( {\frac{{3\sqrt 2 }}{2}} \right)^2} = \frac{{9\pi }}{2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
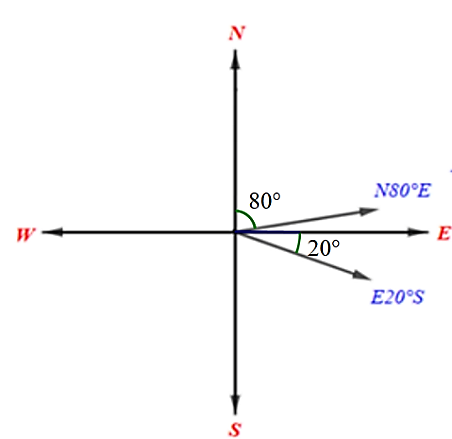
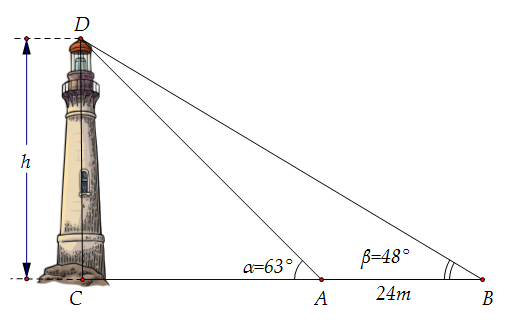
Giả sử tàu du lịch xuất phát từ vị trí \(A\), chuyển động theo hướng \(N80^\circ E\) tới vị trí \(B\) sau đó chuyển hướng \(E80^\circ S\) tới vị trí \(C\) như hình vẽ dưới đây:
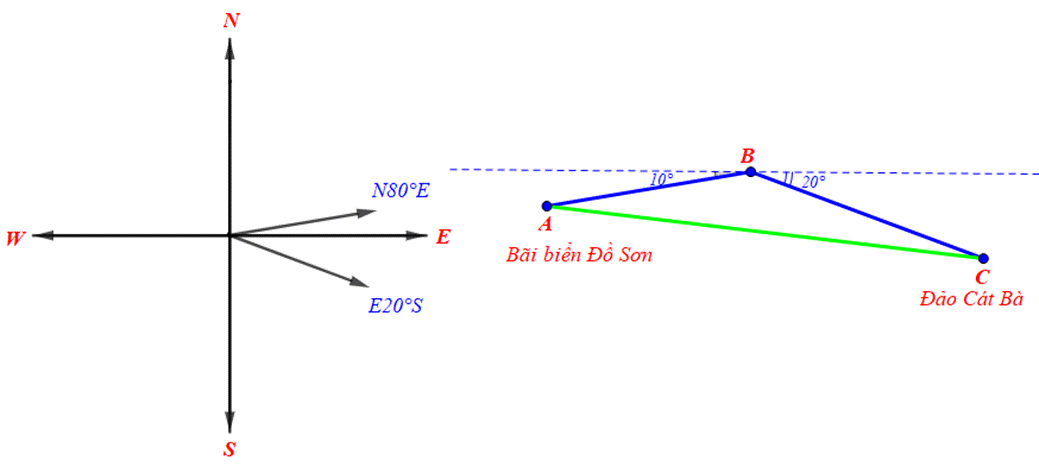
Ta có \(\widehat {ABC} = 180^\circ - 10^\circ - 20^\circ = 150^\circ \).
Tàu chạy từ vị trí \(A\) đến vị trí \(B\) với vận tốc \(20\,\,{\rm{km/h}}\) trong 30 phút (tức 0,5 giờ) nên: \(AB = 20 \cdot 0,5 = 10\) (km).
Tàu chạy từ vị trí \(B\) đến vị trí \(C\) với vận tốc \(20\,\,{\rm{km/h}}\) trong 36 phút (tức 0,6 giờ) nên: \(BC = 20 \cdot 0,6 = 12\) (km).
Áp dụng định lí côsin cho tam giác \(ABC\) ta được:
\(A{C^2} = A{B^2} + B{C^2} - 2AB \cdot AC \cdot \cos \widehat {BAC} = {10^2} + {12^2} - 2 \cdot 10 \cdot 12 \cdot \cos 150^\circ \approx 452\).
Suy ra \(AC \approx \sqrt {452} \approx 21,3\,\,\,\left( {{\rm{km}}} \right)\).
Vậy khi tới đảo Cát Bà thì tàu du lịch cách vị trí xuất phát (bãi biển Đồ Sơn) một khoảng \(21,3\) km. Đáp án: 21,3.
Câu 2
Lời giải
Đáp án đúng là: A
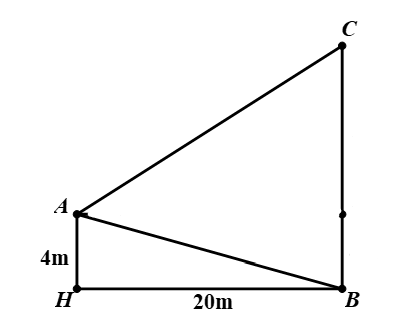
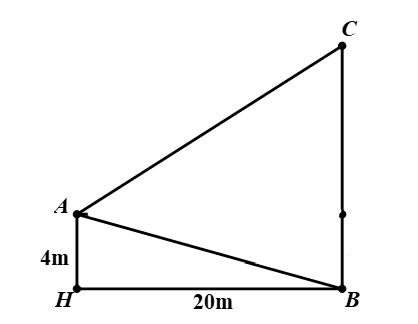
Vì tam giác \[AHB\] vuông tại \[H\] nên ta có \[AB = \sqrt {A{H^2} + H{B^2}} = 4\sqrt {26} \].
Ta có \[\sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{5}{{\sqrt {26} }} \Rightarrow \widehat {BAH} \approx 78,69^\circ \Rightarrow \widehat {ABC} \approx 78,69^\circ \Rightarrow \widehat {ACB} \approx 56,31^\circ \].
Áp dụng định lý sin cho tam giác \[ABC\], ta có \[\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\].
Suy ra \[BC \approx 17,3\] (m).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.