Quảng cáo
Trả lời:
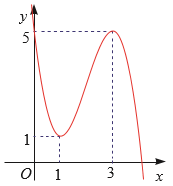
Giả sử hàm số bậc ba cần tìm có dạng \({\rm{y}} = {\rm{f}}({\rm{x}}) = {\rm{a}}{{\rm{x}}^3} + {\rm{b}}{{\rm{x}}^2} + {\rm{cx}} + {\rm{d}}({\rm{a}} \ne 0)\).
Quan sát Hình vẽ , ta thấy đồ thị hàm số đi qua các điềm \((0;5),(1;1)\) và \((3;5)\).
Với \({\rm{x}} = 0\) thì \({\rm{y}} = 5\), thay vào hàm số ta suy ra \({\rm{d}} = 5\).
Khi đó hàm số trở thành \({\rm{y}} = {\rm{f}}({\rm{x}}) = {\rm{a}}{{\rm{x}}^3} + {\rm{b}}{{\rm{x}}^2} + {\rm{cx}} + 5\).
Với \({\rm{x}} = 1\) thì \({\rm{y}} = 1\), thay vào hàm số \({\rm{ta}}\) được \({\rm{a}} + {\rm{b}} + {\rm{c}} + 5 = 1\) (1).
Ta thấy đồ thị hàm số có hai điềm cực trị là \((1;1)\) và \((3;5)\), tức là phương trình \({{\rm{y}}^\prime } = 0\) có hai nghiệm là \({\rm{x}} = 1\) và \({\rm{x}} = 3\).
Ta có \({{\rm{y}}^\prime } = 3{\rm{a}}{{\rm{x}}^2} + 2{\rm{bx}} + {\rm{c}}\).
Với \({\rm{x}} = 1\) thì \({{\rm{y}}^\prime } = 0\) nên ta có \(3{\rm{a}} + 2\;{\rm{b}} + {\rm{c}} = 0\) (2).
Với \({\rm{x}} = 3\) thì \({{\rm{y}}^\prime } = 0\) nên ta có \(27{\rm{a}} + 6\;{\rm{b}} + {\rm{c}} = 0\) (3).
Từ (1), (2) và (3) ta suy ra \({\rm{a}} = - 1;{\rm{b}} = 6;{\rm{c}} = - 9\).
Vậy hàm số cần tìm là \({\rm{y}} = {\rm{f}}({\rm{x}}) = - {{\rm{x}}^3} + 6{{\rm{x}}^2} - 9{\rm{x}} + 5\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1. Tập xác định: D = \[\mathbb{R}\] \ {–1}.
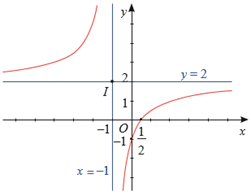
Đồ thị của hàm số giao với trục Ox tại điểm \[\left( { - \frac{1}{2};0} \right)\] và giao với trục Oy tại điểm \[(0; - 1)\].
Đồ thị của hàm số được biểu diễn như hình bên.
Tâm đối xứng của đồ thị hàm số là điểm \[I( - 1;2)\]
Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = -1 và y = 2.