Một con cá hồi bơi ngược dòng nước để vượt một khoảng cách \(300\) km, vận tốc của dòng nước là \(6\) (km/h). Giả sử vận tốc bơi của cá khi nước yên lặng là \(v\) (km/h). Năng lượng tiêu hao của cá trong \(t\) giờ được tính theo công thức \(E = c\,{v^3}t\), \(c\) là hằng số cho trước, đơn vị của \(E\) là Jun. Vận tốc \(v\) của cá khi nước đứng yên để năng lượng của cá tiêu hao ít nhất là

Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(f\left( x \right) = 0,025{x^2}\left( {30 - x} \right)\), trong đó \(x\) (miligam) là liều lượng thuốc được tiêm cho bệnh nhân. Khi đó, liều lượng thuốc được tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là

Một cơ sở sản xuất khăn mặt đang bán mỗ chiếc khăn với giá \(30.000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở đang có kế hoạch tăng giá bán để có lợ nhuận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \[30.000\]đồng mà cứ tăng giá thêm \(1.000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18.000\) đồng. Hỏi cơ sở sản xuất phải bán là mức giá bao nhiêu để đạt lợi nhuận lớn nhất.

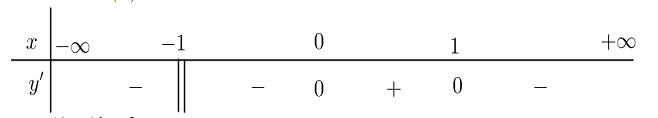
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị của hàm số \(f'\left( x \right)\) trên đoạn \[\left[ { - 2;6} \right]\] như hình vẽ bên.

Tìm khẳng định đúng trong các khẳng định sau.

Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

Mệnh đề nào sau đây đúng

Cho hàm số \(f\left( x \right)\)liên tục trên đoạn \(\left[ { - 3;2} \right]\)và có đồ thị như hình vẽ bên. Gọi \(M,m\)lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 3;2} \right]\). Giá trị của \(M - m\)bằng:

Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\)bằng