Cho tam giác\[ABC\] với trung tuyến \[AM\] và trọng tâm \[G\].
a) \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \).
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {MC} + \overrightarrow {MB} \).
c) Vectơ \(\overrightarrow {AG} + \overrightarrow {GM} \) cùng phương với vectơ \(\overrightarrow {MG} \).
d) \(\overrightarrow {AG} + \overrightarrow {MC} = \overrightarrow {MG} + \overrightarrow {BC} \).
Cho tam giác\[ABC\] với trung tuyến \[AM\] và trọng tâm \[G\].
a) \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \).
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {MC} + \overrightarrow {MB} \).
c) Vectơ \(\overrightarrow {AG} + \overrightarrow {GM} \) cùng phương với vectơ \(\overrightarrow {MG} \).
d) \(\overrightarrow {AG} + \overrightarrow {MC} = \overrightarrow {MG} + \overrightarrow {BC} \).
Quảng cáo
Trả lời:
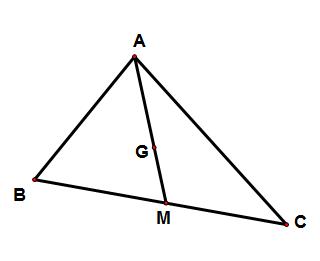
a) Sai. Theo quy tắc hiệu, ta có \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \).
b) Đúng. Vì \[G\] là trọng tâm tam giác\[ABC\] nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
Lại có M là trung điểm của BC nên \(\overrightarrow {MC} + \overrightarrow {MB} = \overrightarrow 0 \).
Vậy \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {MC} + \overrightarrow {MB} \).
c) Đúng. Ta có \(\overrightarrow {AG} + \overrightarrow {GM} = \overrightarrow {AM} \) cùng phương với vectơ \(\overrightarrow {MG} \).
d) Sai. Ta có \(\overrightarrow {AG} + \overrightarrow {MC} = \overrightarrow {MG} + \overrightarrow {BC} \Leftrightarrow \overrightarrow {AG} + \overrightarrow {MC} - \overrightarrow {MG} = \overrightarrow {BC} \Leftrightarrow \overrightarrow {AG} + \overrightarrow {GC} = \overrightarrow {BC} \)
\( \Leftrightarrow \overrightarrow {AC} = \overrightarrow {BC} \Rightarrow A \equiv B\) là sai vì \[A\],\[B\] phân biệt.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
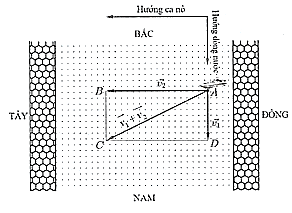
Gọi \(\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} \) lần lượt là vectơ vận tốc của dòng nước đối với bờ và ca nô đối với dòng nước. Khi đó vận tốc của ca nô đối với bờ chính là tổng \(\overrightarrow {{v_1}} + \overrightarrow {{v_2}} \). Đặt \(\overrightarrow {{v_1}} = \overrightarrow {AD} ,\overrightarrow {{v_2}} = \overrightarrow {AB} \) với \(A\) là vị trí của ca nô.
Vẽ hình bình hành \(ABCD\), ta có: \(\overrightarrow {{v_1}} + \overrightarrow {{v_2}} = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} {\rm{. }}\)
Theo định lí Pythagore, ta có: \(AC = \sqrt {{{10}^2} + {{35}^2}} = 5\sqrt {53} \approx 36,4\;\,{\rm{km/h}}{\rm{. }}\)
Vậy vận tốc của ca nô đối với bờ là xấp xỉ \(36,4\;\,{\rm{km/h}}\).
Đáp án: 36,4.
Lời giải
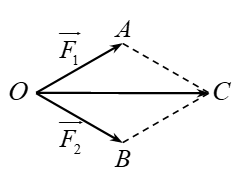
Giả sử \(\overrightarrow {{F_1}} = \overrightarrow {OA} \), \(\overrightarrow {{F_2}} = \overrightarrow {OB} \).
Theo quy tắc hình bình hành, suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OC} \), như hình vẽ.
Ta có \(\widehat {AOB} = 60^\circ \), \(OA = OB = 50\), nên tam giác \(OAB\) đều, suy ra \(OC = 50\sqrt 3 \).
Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {OC} } \right| = 50\sqrt 3 \,\,({\rm{N}}) \approx 86,6\,\,{\rm{(N)}}\).
Đáp án: 86,6.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.