Một con cá hồi bơi ngược dòng nước để vượt một khoảng cách là \(300\;\)km. Vận tốc dòng nước là \(6\)(km/h). Nếu vận tốc bơi của cá khi nước đứng yên là \(v\)(km/h) thì năng lượng tiêu hao của cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c{v^3}t\) (trong đó \(c\) là hằng số dương, \(E\) được tính bằng đơn vị Jun). Cá bơ ngược dòng quãng đường \(300\;\)km trên trong khoảng thời gian \[t\] với vận tốc bằng bao nhiêu để năng lượng tiêu hao là thấp nhất?
Một con cá hồi bơi ngược dòng nước để vượt một khoảng cách là \(300\;\)km. Vận tốc dòng nước là \(6\)(km/h). Nếu vận tốc bơi của cá khi nước đứng yên là \(v\)(km/h) thì năng lượng tiêu hao của cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c{v^3}t\) (trong đó \(c\) là hằng số dương, \(E\) được tính bằng đơn vị Jun). Cá bơ ngược dòng quãng đường \(300\;\)km trên trong khoảng thời gian \[t\] với vận tốc bằng bao nhiêu để năng lượng tiêu hao là thấp nhất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vận tốc khi cá bơi ngược dòng sẽ là \(v - 6\,\)(km/h).
Thời gian để bơi quãng đường \(300\;\)km là \(t = \frac{{300}}{{v - 6}}\left( h \right)\).
Năng lượng tiêu hao là \(E\left( v \right) = 300c\frac{{{v^3}}}{{v - 6}}\,\left( J \right)\).
Do \(c > 0 \Rightarrow E{\left( v \right)_{\min }} \Leftrightarrow \frac{{{v^3}}}{{v - 6}} = {\left( {f\left( v \right)} \right)_{\min }}\).
Với \(v > 6\) ta có \(f'\left( v \right) = \frac{{3{v^2}\left( {v - 6} \right) - {v^3}}}{{{{\left( {v - 6} \right)}^2}}} = \frac{{2{v^3} - 18v}}{{{{\left( {v - 6} \right)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{v = 0}\\{v = 9.}\end{array}} \right.\)
Lập bảng biến thiên ta nhận \(v = 9\) (do \(v > 6\)).
Vậy để năng lượng tiêu hao là thấp nhất thì vận tốc là \(9\)(km/h).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \(x\) là số lần giảm \(0,25\$ \). Cước thuê bao hàng tháng lúc này là \(40 - 0,25x\) với \(0 \le x \le 160\) (do mức cước không thể âm), và số thuê bao mới là \(1000x\).
Do đó, tổng số thuê bao là \(100000 + 1000x\).
Hàm doanh thu được cho bởi R = (số thuê bao) x (cước mỗi thuê bao trả)
\[R = \left( {100000 + 1000x} \right)\left( {40 - 0,25x} \right) = 1000\left( {100 + x} \right)\left( {40 - 0,25x} \right) = 1000\left( {4000 + 15x - 0,25{x^2}} \right)\]
Đạo hàm \(R' = 0\), ta được \(R' = 1000\left( {15 - 0,5x} \right) = 0 \Leftrightarrow x = 30.{\rm{ }}\)
Vì tập xác định của \(R\) là khoảng đóng [0; 160] nên \(R\) đạt cực đại tại \(x = 30\) hoặc tại các điểm đầu mút của đoạn [0; 160].
Ta có: \[R\left( 0 \right) = 4000000;\,\,R\left( {30} \right) = 4225000\,;\,\,R\left( {160} \right) = 0\]
Vậy doanh thu tối đa khi \(x = 30\). Điều này tương ứng với 30 lần giảm \(0,25\$ \), tức là cước thuê bao hàng tháng là \(40\$ - 7,5\$ = 32,5\$ \).
Số thuê bao tại mức cước này là \(100000 + 30.\left( {1000} \right) = 130000\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi độ dài đoạn dây gấp tam giác đều là \(x\) thì độ dài đoạn dây gấp hình vuông là \(60 - x\)(mét)
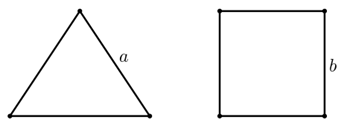
Khi đó \(x = 3a \Leftrightarrow a = \frac{x}{3} \Rightarrow {S_1} = \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{x^2}\sqrt 3 }}{{36}}\)
Mặt khác: \(60 - x = 4b \Rightarrow b = \frac{{60 - x}}{4} \Rightarrow {S^2} = {b^2} = {\left( {\frac{{60 - x}}{4}} \right)^2}\)
Khi đó \({S_1} + {S_2} = \frac{{{x^2}\sqrt 3 }}{{36}} + {\left( {\frac{{60 - x}}{4}} \right)^2} \Leftrightarrow f\left( x \right) = \frac{{\left( {9 + 4\sqrt 3 } \right){x^2} - 1080x + 32400}}{{144}}\)
Dễ dàng tính được \({\left( {{S_1} + {S_2}} \right)_{\min }} = \min \,f\left( x \right) = f\left( {\frac{{540}}{{9 + 4\sqrt 3 }}} \right) \approx 97,87\,\left( {{{\rm{m}}^2}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập