Một công ty đánh giá rằng sẽ bán được $N$ lô hàng nếu chi hết số tiền là $x$ (triệu đồng) vào việc quảng cáo. Biết rằng $N$ và $x$ liên hệ với nhau bằng biểu thức $N\left( x \right) = - {x^2} + 30x + 6,0 \le x \le 30$. Hãy tìm số lô hàng lớn nhất mà công ti có thể bán sau đợt quảng cáo?

Câu hỏi trong đề: (Trả lời ngắn) 23 bài tập Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có $N\left( x \right) = - {x^2} + 30x + 6 \Rightarrow N'\left( x \right) = - 2x + 30 \Rightarrow N'\left( x \right) = 0 \Leftrightarrow x = 15.$

Đồng thời, ta cũng có $\left\{ {\begin{array}{*{20}{l}}{N\left( 0 \right) = 6}\\{N\left( {15} \right) = 231}\\{N\left( {30} \right) = 6}\end{array} \Rightarrow {{\max }_{x \in [0;30]}}N\left( x \right) = 231 \Leftrightarrow x = 15.} \right.$

Vậy nếu công ti dành 15 triệu cho việc quảng cáo thì công ti sẽ bán được nhiều nhất là 231 lô hàng.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Công ti truyền hình cáp Vista hiện có 100000 thuê bao. Mỗi thuê bao đang trả cước thuê bao 40$/ tháng. Một cuộc khảo sát cho thấy cứ mỗi lần giảm $0,25 $$ cước thuê bao, công ti có thể có thêm 1000 thuê bao. Để doanh thu thu được là tối đa, công ti cần xác định mức cước thuê bao mỗi tháng là bao nhiêu?

Xem đáp án

Lời giải

Gọi $x$ là số lần giảm $0,25\$ $. Cước thuê bao hàng tháng lúc này là $40 - 0,25x$ với $0 \le x \le 160$ (do mức cước không thể âm), và số thuê bao mới là $1000x$.

Do đó, tổng số thuê bao là $100000 + 1000x$.

Hàm doanh thu được cho bởi R = (số thuê bao) x (cước mỗi thuê bao trả)

\[R = \left( {100000 + 1000x} \right)\left( {40 - 0,25x} \right) = 1000\left( {100 + x} \right)\left( {40 - 0,25x} \right) = 1000\left( {4000 + 15x - 0,25{x^2}} \right)\]

Đạo hàm $R' = 0$, ta được $R' = 1000\left( {15 - 0,5x} \right) = 0 \Leftrightarrow x = 30.{\rm{ }}$

Vì tập xác định của $R$ là khoảng đóng [0; 160] nên $R$ đạt cực đại tại $x = 30$ hoặc tại các điểm đầu mút của đoạn [0; 160].

Ta có: \[R\left( 0 \right) = 4000000;\,\,R\left( {30} \right) = 4225000\,;\,\,R\left( {160} \right) = 0\]

Vậy doanh thu tối đa khi $x = 30$. Điều này tương ứng với 30 lần giảm $0,25\$ $, tức là cước thuê bao hàng tháng là $40\$ - 7,5\$ = 32,5\$ $.

Số thuê bao tại mức cước này là $100000 + 30.\left( {1000} \right) = 130000$.

Câu 2

Cắt một đoạn dây dài $60{\rm{m}}$thành hai đoạn dây, đoạn dây thứ nhất gấp thành một tam giác đều có diện tích ${S_1}$, đoạn dây thứ hai gấp thành một hình vuông có diện tích ${S_2}$ (như hình vẽ dưới)

Khi đó giá trị nhỏ nhất của tổng $T = {S_1} + {S_2}$ là bao nhiêu?

Xem đáp án

Lời giải

Gọi độ dài đoạn dây gấp tam giác đều là $x$ thì độ dài đoạn dây gấp hình vuông là $60 - x$(mét)

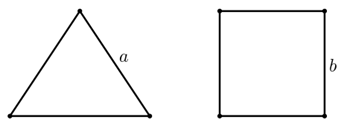
(Trả lời ngắn) Cắt một đoạn dây dài thành hai đoạn dây, đoạn dây thứ nhất gấp thành một tam giác đều có diện tích s1 (ảnh 2)

Khi đó $x = 3a \Leftrightarrow a = \frac{x}{3} \Rightarrow {S_1} = \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{x^2}\sqrt 3 }}{{36}}$

Mặt khác: $60 - x = 4b \Rightarrow b = \frac{{60 - x}}{4} \Rightarrow {S^2} = {b^2} = {\left( {\frac{{60 - x}}{4}} \right)^2}$

Khi đó ${S_1} + {S_2} = \frac{{{x^2}\sqrt 3 }}{{36}} + {\left( {\frac{{60 - x}}{4}} \right)^2} \Leftrightarrow f\left( x \right) = \frac{{\left( {9 + 4\sqrt 3 } \right){x^2} - 1080x + 32400}}{{144}}$

Dễ dàng tính được ${\left( {{S_1} + {S_2}} \right)_{\min }} = \min \,f\left( x \right) = f\left( {\frac{{540}}{{9 + 4\sqrt 3 }}} \right) \approx 97,87\,\left( {{{\rm{m}}^2}} \right)$.

Câu 3