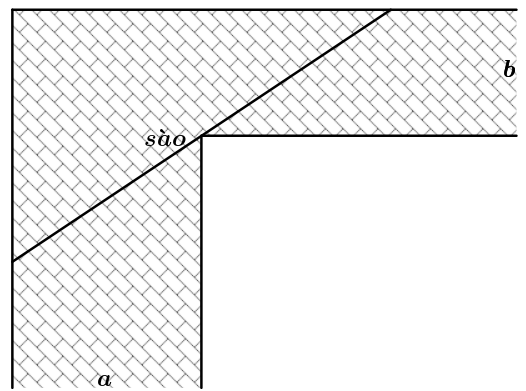
Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết \[a = 24\] và \[b = 3\]. Hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?

Quảng cáo
Trả lời:
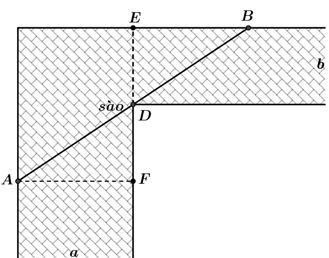
Đặt các điểm như hình vẽ.
Đặt \(DF = x\), \(x > 0\), ta có \(\Delta ADF\) đồng dạng với \(\Delta BED\) nên \(\frac{{EB}}{{ED}} = \frac{{AF}}{{DF}}\)\( \Rightarrow EB = \frac{{ab}}{x}\)
Gọi \[l\] là chiều dài của que sào, ta có \({l^2} = A{B^2} = {\left( {x + b} \right)^2} + {\left( {a + \frac{{ab}}{x}} \right)^2} = f\left( x \right)\).
Đạo hàm: \(f'\left( x \right) = 2\left( {x + b} \right) - 2\frac{{ab}}{{{x^2}}}\left( {a + \frac{{ab}}{x}} \right) = 2\left( {x + b} \right)\left( {1 - \frac{{{a^2}b}}{{{x^3}}}} \right)\); \(f'\left( x \right) = 0 \Leftrightarrow x = \sqrt[3]{{{a^2}b}} = 12\).
Dễ dàng suy ra được \(\min \,f\left( x \right) = f\left( {12} \right) = 1125\)
Vậy giá trị nhỏ nhất của que sào là \(l = \sqrt {1125} = 15\sqrt 5 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số lần giảm \(0,25\$ \). Cước thuê bao hàng tháng lúc này là \(40 - 0,25x\) với \(0 \le x \le 160\) (do mức cước không thể âm), và số thuê bao mới là \(1000x\).
Do đó, tổng số thuê bao là \(100000 + 1000x\).
Hàm doanh thu được cho bởi R = (số thuê bao) x (cước mỗi thuê bao trả)
\[R = \left( {100000 + 1000x} \right)\left( {40 - 0,25x} \right) = 1000\left( {100 + x} \right)\left( {40 - 0,25x} \right) = 1000\left( {4000 + 15x - 0,25{x^2}} \right)\]
Đạo hàm \(R' = 0\), ta được \(R' = 1000\left( {15 - 0,5x} \right) = 0 \Leftrightarrow x = 30.{\rm{ }}\)
Vì tập xác định của \(R\) là khoảng đóng [0; 160] nên \(R\) đạt cực đại tại \(x = 30\) hoặc tại các điểm đầu mút của đoạn [0; 160].
Ta có: \[R\left( 0 \right) = 4000000;\,\,R\left( {30} \right) = 4225000\,;\,\,R\left( {160} \right) = 0\]
Vậy doanh thu tối đa khi \(x = 30\). Điều này tương ứng với 30 lần giảm \(0,25\$ \), tức là cước thuê bao hàng tháng là \(40\$ - 7,5\$ = 32,5\$ \).
Số thuê bao tại mức cước này là \(100000 + 30.\left( {1000} \right) = 130000\).
Lời giải
Gọi độ dài đoạn dây gấp tam giác đều là \(x\) thì độ dài đoạn dây gấp hình vuông là \(60 - x\)(mét)
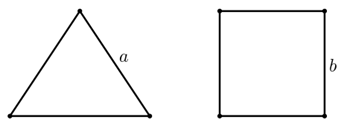
Khi đó \(x = 3a \Leftrightarrow a = \frac{x}{3} \Rightarrow {S_1} = \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{x^2}\sqrt 3 }}{{36}}\)
Mặt khác: \(60 - x = 4b \Rightarrow b = \frac{{60 - x}}{4} \Rightarrow {S^2} = {b^2} = {\left( {\frac{{60 - x}}{4}} \right)^2}\)
Khi đó \({S_1} + {S_2} = \frac{{{x^2}\sqrt 3 }}{{36}} + {\left( {\frac{{60 - x}}{4}} \right)^2} \Leftrightarrow f\left( x \right) = \frac{{\left( {9 + 4\sqrt 3 } \right){x^2} - 1080x + 32400}}{{144}}\)
Dễ dàng tính được \({\left( {{S_1} + {S_2}} \right)_{\min }} = \min \,f\left( x \right) = f\left( {\frac{{540}}{{9 + 4\sqrt 3 }}} \right) \approx 97,87\,\left( {{{\rm{m}}^2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.