Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?
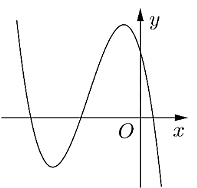
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?
A. 4.
B. 2.
C. 1.
D. 3.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn C
Ta thấy đồ thị hàm số cắt trục tung tại điểm có tung độ dương. Suy ra d > 0.
$\mathop {\lim }\limits_{x \to - \infty } y = + \infty \Rightarrow a < 0$
Ta có y' = 3ax2 + 2bx + c.
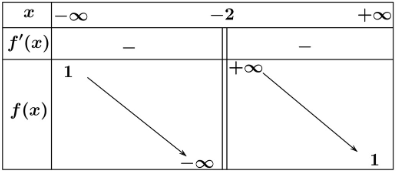
Điểm cực đại và cực tiểu của hàm số đều âm nên
$\left\{ \begin{array}{l}
- \frac{{2b}}{{3a}} < 0\\
\frac{c}{{3a}} > 0
\end{array} \right.$
- \frac{{2b}}{{3a}} < 0\\
\frac{c}{{3a}} > 0
\end{array} \right.$
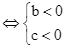(vì a < 0).
Do đó có 1 số dương.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 
.
.B. 
.
. C. 
.
.D. 
.
.Lời giải
Chọn A
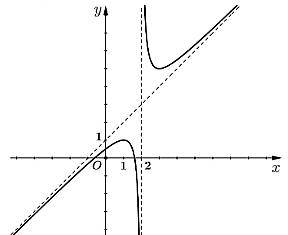
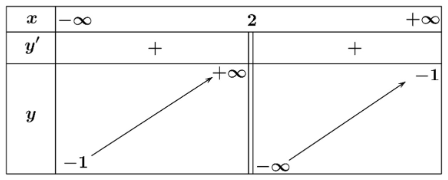
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số nhận x = 2 làm tiệm cận đứng và y = x + 1 làm tiệm cận xiên.
Xét hàm số 
.
Vì 
nên y = x + 1 là tiệm cận xiên của đồ thị hàm số.
Lời giải
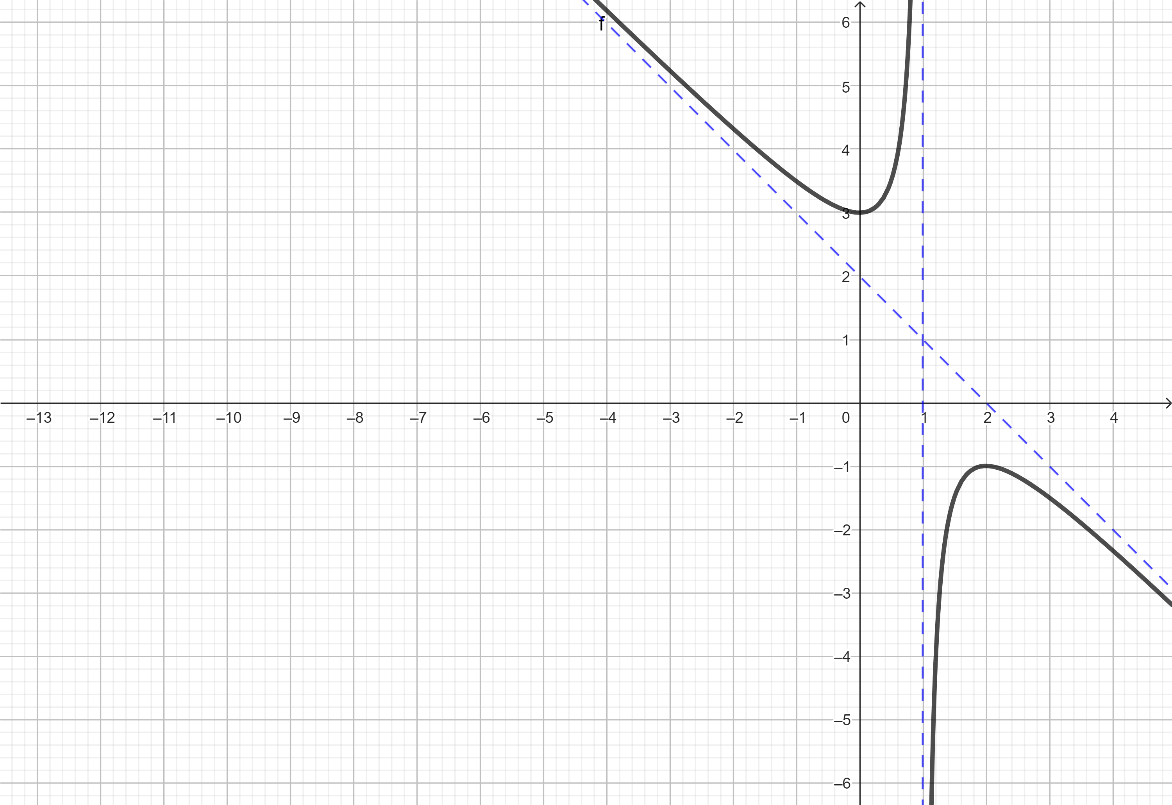
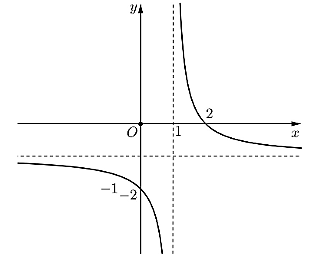
Ta có 
nên đồ thị hàm số nhận hai đường thẳng x = 1 và y = 5x – 1 tương ứng là tiệm cận đứng và tiệm cận xiên.
Suy ra a = 1; b = 4 Þ a + 3b = 1 + 3.4 = 13.
Trả lời: 13.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. S = 0.
B. S = −2.
C. S = 2.
D. S = 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 3.
B. 1.
C. 2.
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo