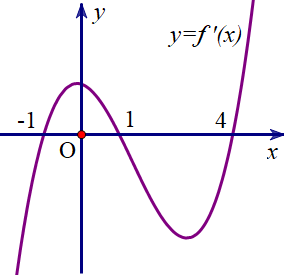
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ dưới đây:
a) Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
c) \(f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)\).
d) Trên đoạn \(\left[ { - 1;4} \right]\), giá trị lớn nhất của hàm số \(y = f\left( x \right)\) là \(f\left( 1 \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ dưới đây:

a) Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
c) \(f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)\).
d) Trên đoạn \(\left[ { - 1;4} \right]\), giá trị lớn nhất của hàm số \(y = f\left( x \right)\) là \(f\left( 1 \right)\).
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Kết nối tri thức Chương 1 có đáp án !!
Quảng cáo
Trả lời:
Từ đồ thị của hàm số \(y = f'\left( x \right)\) ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau:
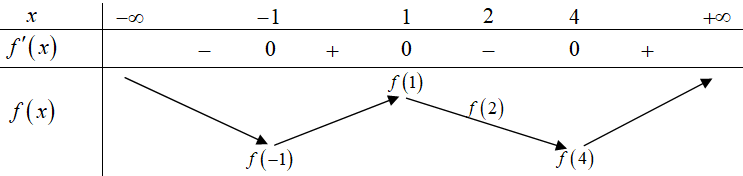
Khi đó dựa vào bảng biến thiên ta thấy:
a) Sai. Hàm số có ba điểm cực trị.
b) Sai. Hàm số đồng biến trên các khoảng \(\left( { - 1;1} \right)\) và \(\left( {4; + \infty } \right)\).
c) Đúng. Hàm số nghịch biến trên khoảng \(\left( {1;4} \right)\)nên \(f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)\).
d) Đúng. Trên đoạn \(\left[ { - 1;4} \right]\), giá trị lớn nhất của hàm số \(y = f\left( x \right)\) là \(f\left( 1 \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Chi phí mỗi ngày là tổng các chi phí nên \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\) (triệu đồng).
b) Sai. Khi \(x = 100\), ta có \(C\left( {100} \right) = 0,0005 \times {100^2} + 0,15 \times 100 + 5 = 25\).
c) Sai. Chi phí trung bình trên mỗi khối sản phẩm là:
\(\overline c \left( x \right) = \frac{{0,0005{x^2} + 0,15x + 5}}{x} = 0,0005x + 0,15 + \frac{5}{x}\).
d) Đúng. Xét hàm số \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\), \(0 < x \le 200\).
Ta có \({\overline c ^{\,\prime }}\left( x \right) = \frac{5}{{{{10}^4}}} - \frac{5}{{{x^2}}}\), \({\overline c ^\prime }\left( x \right) = 0 \Leftrightarrow {x^2} = {10^4} \Rightarrow x = 100\) (do \(x \in \left( {0;200} \right]\)
Bảng biến thiên:
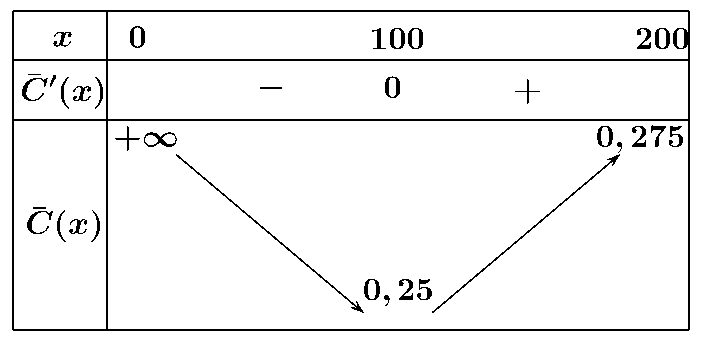
Câu 2
Lời giải
Chọn C
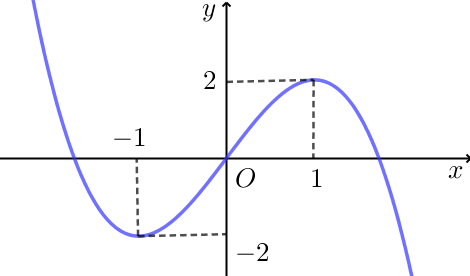
Ta có \(f\left( x \right) = 2\,\,\,\left( * \right)\).
Số nghiệm của phương trình \(\left( * \right)\) bằng số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 2\).
Dựa vào hình vẽ, hai đồ thị cắt nhau tại hai điểm.
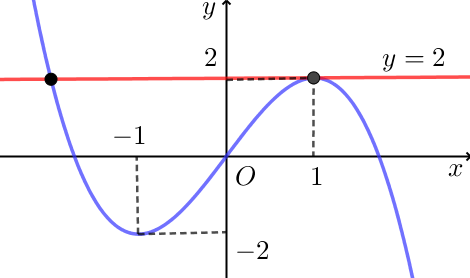
Vậy phương trình \(f\left( x \right) = 2\) có hai nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.