Giả sử doanh số bán hàng (đơn vị triệu đồng) của một sản phẩm mới trong vòng một số năm nhất định tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = 500\left( {{t^2} + m{e^{ - t}}} \right)\), với \(t \ge 0\) là thời gian tính bằng năm kể từ khi phát hành sản phẩm mới, \(m \le 0\) là tham số. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ bán hàng. Biết rằng tốc độ bán hàng luôn tăng trong khoảng thời gian 10 năm đầu phát hành sản phẩm, khi đó giá trị nhỏ nhất của \(m\) bằng bao nhiêu?
Giả sử doanh số bán hàng (đơn vị triệu đồng) của một sản phẩm mới trong vòng một số năm nhất định tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = 500\left( {{t^2} + m{e^{ - t}}} \right)\), với \(t \ge 0\) là thời gian tính bằng năm kể từ khi phát hành sản phẩm mới, \(m \le 0\) là tham số. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ bán hàng. Biết rằng tốc độ bán hàng luôn tăng trong khoảng thời gian 10 năm đầu phát hành sản phẩm, khi đó giá trị nhỏ nhất của \(m\) bằng bao nhiêu?
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Kết nối tri thức Chương 1 có đáp án !!
Quảng cáo
Trả lời:
Ta có \(f'\left( t \right) = 500\left( {2t - m{e^{ - t}}} \right)\) và \[f''\left( t \right) = 500\left( {2 + m{e^{ - t}}} \right)\]
Tốc độ bán hàng luôn tăng trong khoảng thời gian 10 năm đầu phát hành sản phẩm.\( \Leftrightarrow f'\left( t \right)\). là hàm số đồng biến trên \(\left[ {0\,;\,10} \right]\) \( \Leftrightarrow f''\left( t \right) \ge 0\), \(\forall t \in \left[ {0\,;\,10} \right]\)\( \Leftrightarrow \)\[500\left( {2 + m{e^{ - t}}} \right) \ge 0\,,\,\,\forall t \in \left[ {0\,;\,10} \right]\]
\( \Leftrightarrow \)\[2 + m{e^{ - t}} \ge 0\,,\,\,\forall t \in \left[ {0\,;\,10} \right]\]\( \Leftrightarrow \)\[m{e^{ - t}} \ge - 2\,,\,\,\forall t \in \left[ {0\,;\,10} \right]\]\( \Leftrightarrow m \ge - 2{e^t}\,,\,\,\forall t \in \left[ {0\,;\,10} \right]\)
\( \Leftrightarrow m \ge - 2{e^0} = - 2\) (do hàm số \(y = - 2{e^t}\) nghịch biến trên \(\left[ {0\,;\,10} \right]\)).
Vậy giá trị nhỏ nhất của \(m\) là \( - 2\).
Đáp án: −2.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
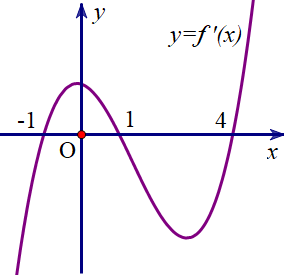
Từ đồ thị của hàm số \(y = f'\left( x \right)\) ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau:
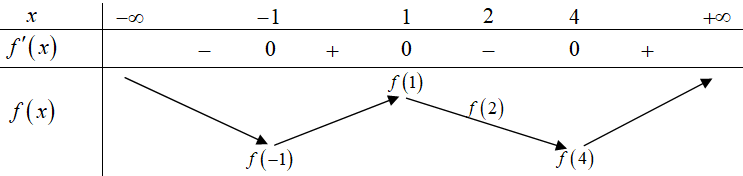
Khi đó dựa vào bảng biến thiên ta thấy:
a) Sai. Hàm số có ba điểm cực trị.
b) Sai. Hàm số đồng biến trên các khoảng \(\left( { - 1;1} \right)\) và \(\left( {4; + \infty } \right)\).
c) Đúng. Hàm số nghịch biến trên khoảng \(\left( {1;4} \right)\)nên \(f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)\).
d) Đúng. Trên đoạn \(\left[ { - 1;4} \right]\), giá trị lớn nhất của hàm số \(y = f\left( x \right)\) là \(f\left( 1 \right)\).
Lời giải
a) Đúng. Chi phí mỗi ngày là tổng các chi phí nên \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\) (triệu đồng).
b) Sai. Khi \(x = 100\), ta có \(C\left( {100} \right) = 0,0005 \times {100^2} + 0,15 \times 100 + 5 = 25\).
c) Sai. Chi phí trung bình trên mỗi khối sản phẩm là:
\(\overline c \left( x \right) = \frac{{0,0005{x^2} + 0,15x + 5}}{x} = 0,0005x + 0,15 + \frac{5}{x}\).
d) Đúng. Xét hàm số \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\), \(0 < x \le 200\).
Ta có \({\overline c ^{\,\prime }}\left( x \right) = \frac{5}{{{{10}^4}}} - \frac{5}{{{x^2}}}\), \({\overline c ^\prime }\left( x \right) = 0 \Leftrightarrow {x^2} = {10^4} \Rightarrow x = 100\) (do \(x \in \left( {0;200} \right]\)
Bảng biến thiên:
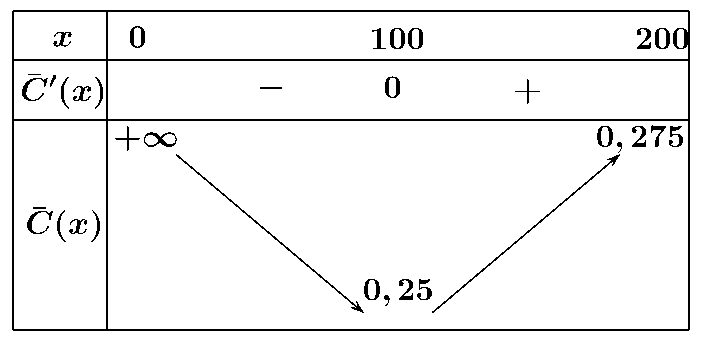
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.