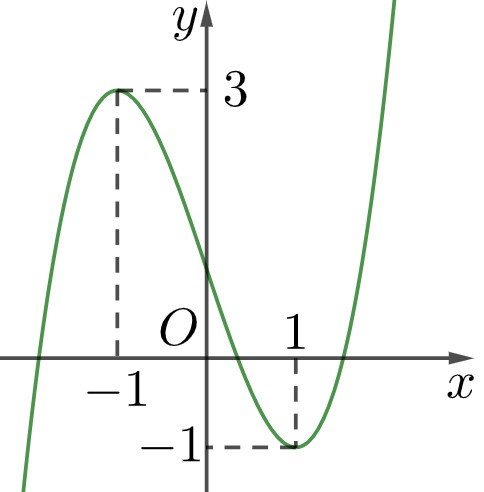
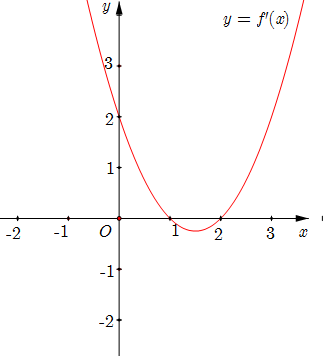
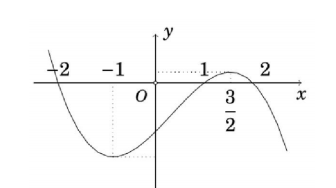
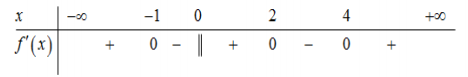Cho hàm số \(y = f(x)\) có bảng biến thiên như hình dưới:
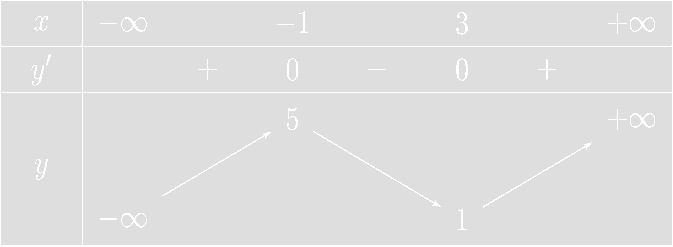
Số điểm cực trị của hàm số \(y = f\left( {{x^2} - 4x + 1} \right)\) là:
Cho hàm số \(y = f(x)\) có bảng biến thiên như hình dưới:

Quảng cáo
Trả lời:
Ta có \(g\left( x \right) = f\left( {{x^2} - 4x + 1} \right)\).
\( \Rightarrow g'\left( x \right) = {\left( {{x^2} - 4x + 1} \right)^\prime }.f'\left( {{x^2} - 4x + 1} \right) = 2\left( {x - 2} \right).f'\left( {{x^2} - 4x + 1} \right)\).
Ta có \[g'\left( x \right) = 0 \Leftrightarrow 2\left( {x - 2} \right).f'\left( {{x^2} - 4x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\{x^2} - 4x + 1 = - 1\\{x^2} - 4x + 1 = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 2 - \sqrt 2 \\x = 2 + \sqrt 2 \\x = 2 - \sqrt 6 \\x = 2 + \sqrt 6 \end{array} \right.\].
Ta có bảng xét dấu của \(g'\left( x \right)\).

Dựavào bảng biến thiên ta thấy hàm số \(g\left( x \right) = f\left( {{x^2} - 4x + 1} \right)\) có 5 điểm cực trị.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
TXĐ: \(D = \mathbb{R}\).
Có \(y = \sqrt {{x^2} + 1} - mx - 1 \Rightarrow y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m\).
Theo yêu cầu bài toán: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m \ge 0{\rm{, }}\forall x \in \mathbb{R}\)\( \Leftrightarrow m \le \frac{x}{{\sqrt {{x^2} + 1} }},{\rm{ }}\forall x \in \mathbb{R}{\rm{ }}\left( 1 \right)\).
Xét hàm số \(g\left( x \right) = \frac{x}{{\sqrt {{x^2} + 1} }}\) với \[x \in \mathbb{R}\]. Ta có \(g'\left( x \right) = \frac{1}{{\sqrt {{x^2} + 1} \left( {{x^2} + 1} \right)}} > 0,{\rm{ }}\forall x \in \mathbb{R}\).
Bảng biến thiên
![Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2024;2024} \right]\) để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên \(\mathbb{R}\). A. \(2024\). B. \(2019\). C. \(2020\). D. \(0\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759133862.png)
Từ \(\left( 1 \right) \Rightarrow m \le - 1\) mà \(\left\{ \begin{array}{l}m \in \left[ { - 2024;2024} \right]\\m \in \mathbb{Z}\end{array} \right.\) nên có 2024 giá trị nguyên.
Lời giải
Diện tích của đáy hộp là: \(S = \frac{V}{h} = \frac{{96.000}}{{60}} = 1600c{m^2} = 0,16{m^2}\)
Gọi chiều dài cạnh đáy của hộp là \(x,\left( {x > 0,m} \right)\)
Chiều rộng của hộp là \(\frac{{0,16}}{x}\)
Gọi \(F\left( x \right)\) là hàm chi phí để làm để cá.
Chi phí để hoàn thành bể cá:
\[\begin{array}{l}F\left( x \right) = 0,16 \times 100.000 + 2.0,6x.70.000 + 2.0,6.\frac{{0,16}}{x}.70.000\\ = 16.000 + 48.000x + \frac{{13440}}{x}\end{array}\]
Câu toán trở thành tìm x để F đạt GTNN.
\(\begin{array}{l}F'\left( x \right) = 84.000 - \frac{{13440}}{{{x^2}}}\\F'\left( x \right) = 0 \Leftrightarrow 84.000 - \frac{{13440}}{{{x^2}}} = 0 \Leftrightarrow x = 0,4\end{array}\)
Bảng biến thiên:
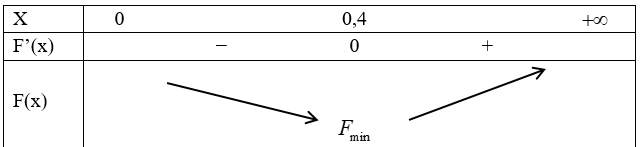
Vậy chi phí thấp nhất để hoàn thành bể cá là: 83.200 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.