khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

29/09/2025 811 Lưu

Cho hàm số \(y = \frac{{2{x^2} + 2x - 1 - 5m}}{{x - m}}\)

a) Hàm số xác định với mọi \(x\).

b) Có 2019 giá trị nguyên dương bé hơn 2024 của tham số \(m\)để  hàm số \(y = \frac{{2{x^2} + 2x - 1 - 5m}}{{x - m}}\) nghịch biến trên khoảng \(\left( {1;5} \right)\).

c) \(m = 0\) thì hàm số có hai cực trị.

d) Nếu đồ thị hàm số có hai điểm cực trị thì hai điểm cực trị đó luôn nằm trên đường thẳng cố định.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra Tính đơn điệu và cực trị của hàm số lớp 12 (có lời giải) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a) Sai. Tập xác định \[D = \mathbb{R}\backslash \left\{ m \right\}\]

b) Đúng Tập xác định \[D = \mathbb{R}\backslash \left\{ m \right\}\] và có \(y' = \frac{{2{x^2} - 4mx + 3m + 1}}{{{{\left( {x - m} \right)}^2}}}\).

Hàm số nghịch biến trên khoảng \(\left( {1;5} \right)\)

\( \Leftrightarrow y' = \frac{{2{x^2} - 4mx + 3m + 1}}{{{{\left( {x - m} \right)}^2}}} \le 0\forall x \in \left( {1;5} \right) \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - 4mx + 3m + 1 \le 0\forall x \in \left( {1;5} \right)\\m \notin \left( {1;5} \right)\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l} - m + 3 \le 0\\ - 17m + 51 \le 0\\\left[ \begin{array}{l}m \le 1\\m \ge 5\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge 3\\m \ge 3\\\left[ \begin{array}{l}m \le 1\\m \ge 5\end{array} \right.\end{array} \right. \Leftrightarrow m \ge 5\)

Do nguyên dương bé hơn 2024 nên \(5 \le m \le 2023\). Vậy có tất cả 2019 giá trị.

c) Sai. Với \(m = 0\) thì \(y' = \frac{{2{x^2} + 1}}{{{x^2}}} > 0\,\forall x \ne 0\)

Vậy hàm số không có cực trị với \(m = 0\).

d) Đúng. Giả sử đồ thị hàm số có hai điểm cực trị khi đó hai điểm cực trị hàm số luôn nằm trên   đường thẳng \(y = 4x + 2\)

Chú ý:

Áp dụng tính chất: Nếu \[{x_0}\] là điểm cực trị của hàm số hữu tỷ \[y = \frac{{u\left( x \right)}}{{v\left( x \right)}}\] thì giá trị cực trị tương ứng của hàm số là \[{y_0} = \frac{{u\left( {{x_0}} \right)}}{{v\left( {{x_0}} \right)}} = \frac{{u'\left( {{x_0}} \right)}}{{v'\left( {{x_0}} \right)}}\]. Suy ra với bài toán trên ta có phương trình đường thẳng qua hai điểm cực trị của đồ thị hàm số là \[y = \frac{{{{\left( {2{x^2} + 2x - 1 - 5m} \right)}^\prime }}}{{{{\left( {x - m} \right)}^\prime }}} = 4x + 2\].

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2024;2024} \right]\) để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên \(\mathbb{R}\).
A. \(2024\).                          
B. \(2019\).                        
C. \(2020\).                                
D. \(0\).

Lời giải

TXĐ: \(D = \mathbb{R}\).

Có \(y = \sqrt {{x^2} + 1}  - mx - 1 \Rightarrow y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m\).

Theo yêu cầu bài toán: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m \ge 0{\rm{, }}\forall x \in \mathbb{R}\)\( \Leftrightarrow m \le \frac{x}{{\sqrt {{x^2} + 1} }},{\rm{ }}\forall x \in \mathbb{R}{\rm{ }}\left( 1 \right)\).

Xét hàm số \(g\left( x \right) = \frac{x}{{\sqrt {{x^2} + 1} }}\) với \[x \in \mathbb{R}\]. Ta có \(g'\left( x \right) = \frac{1}{{\sqrt {{x^2} + 1} \left( {{x^2} + 1} \right)}} > 0,{\rm{ }}\forall x \in \mathbb{R}\).

Bảng biến thiên

Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2024;2024} \right]\) để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên \(\mathbb{R}\). A. \(2024\). B. \(2019\). C. \(2020\). D. \(0\). (ảnh 1)

Từ \(\left( 1 \right) \Rightarrow m \le  - 1\) mà \(\left\{ \begin{array}{l}m \in \left[ { - 2024;2024} \right]\\m \in \mathbb{Z}\end{array} \right.\) nên có 2024 giá trị nguyên.

Câu 2

Để thiết kế một chiếc bể cá hình chữ nhật có chiều cao là \(60cm,\) thể tích là \(96.000c{m^3}\), người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70.000 đồng/m2 và loại kính để làm mặt đáy có giá thành là 100.000 đồng/m2. Tính chi phí thấp nhất để hoàn thành bể cá.

Lời giải

Diện tích của đáy hộp là: \(S = \frac{V}{h} = \frac{{96.000}}{{60}} = 1600c{m^2} = 0,16{m^2}\)

Gọi chiều dài cạnh đáy của hộp là \(x,\left( {x > 0,m} \right)\)

Chiều rộng của hộp là \(\frac{{0,16}}{x}\)

Gọi \(F\left( x \right)\) là hàm chi phí để làm để cá.

Chi phí để hoàn thành bể cá:

\[\begin{array}{l}F\left( x \right) = 0,16 \times 100.000 + 2.0,6x.70.000 + 2.0,6.\frac{{0,16}}{x}.70.000\\ = 16.000 + 48.000x + \frac{{13440}}{x}\end{array}\]

Câu toán trở thành tìm x để F đạt GTNN.

\(\begin{array}{l}F'\left( x \right) = 84.000 - \frac{{13440}}{{{x^2}}}\\F'\left( x \right) = 0 \Leftrightarrow 84.000 - \frac{{13440}}{{{x^2}}} = 0 \Leftrightarrow x = 0,4\end{array}\)

Bảng biến thiên:

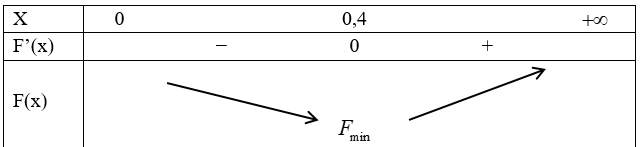
Tính chi phí thấp nhất để hoàn thành bể cá. (ảnh 1)

Vậy chi phí thấp nhất để hoàn thành bể cá là: 83.200 đồng.

Câu 3

Có bao nhiêu giá trị nguyên của \(m\) thuộc đoạn \(\left[ { - 8;8} \right]\) để hàm số \(y = \left| {{x^3} - 3\left( {m + 2} \right){x^2} + 3m\left( {m + 4} \right)x + 5} \right|\) đồng biến trên khoảng \(\left( {1;3} \right)\)?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình sau. Hàm số \(g\left( x \right) = f\left( {3 - 2x} \right) + 2024\) đồng biến trên khoảng nào dưới đây?

Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình sau. Hàm số \(g\left( x \right) = f\left( {3 - 2x} \right) + 2024\) đồng biến trên khoảng nào dưới đây? (ảnh 1)
A. \(\left( {1; + \infty } \right)\).                                
B. \(\left( {\frac{1}{2};1} \right)\).                                             
C. \(\left( {0;\frac{1}{2}} \right)\).                                             
D. \(\left( { - \infty ;\frac{1}{2}} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f\left( 2 \right) = f\left( { - 2} \right) = 0\) và đồ thị hàm số \(y = f'\left( x \right)\) có dạng như hình vẽ bên dưới.

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f\left( 2 \right) = f\left( { - 2} \right) = 0\) v (ảnh 1)

Hàm số \(g\left( x \right) = {\left( {f\left( x \right)} \right)^2}\) nghịch biến trên khoảng nào dưới đây?
A. \(\left( { - 2; - 1} \right)\).                                       
B. \(\left( { - 1;\frac{3}{2}} \right)\).  
C. \(\left( { - 1;1} \right)\).                                
D. \(\left( {1;2} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số \(y = f(x)\) liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ.

Hàm số đã cho có bao nhiêu điểm cực trị? (ảnh 1)

Hàm số đã cho có bao nhiêu điểm cực trị?                    
A. \(4\).                                   
B. \(1\).                                   
C. \(3\).           
D. \(2\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số bậc ba \(y = f(x)\) có đồ thị là đường cong như hình vẽ sau

Cho hàm số bậc ba \(y = f(x)\) có đồ thị là đường cong như hình vẽ sau (ảnh 1)

Mỗi khẳng định sau đây đúng hay sai?

a) Hàm số \(y = f(x)\)đồng biến trên khoảng \(( - \infty ;3).\)

b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số \(y = f(x)\) là 2.

c) Hàm số \(y = f(x)\)có hai cực trị trái dấu.

d) Phương trình đường thẳng qua 2 điểm cực trị của đồ thị hàm số \(y = f(x)\) là \[d:y = - 3x\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập