Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Diện tích lớn nhất của đất rào thu được là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \[x\]là chiều dài 1 mặt hàng rào hình chữ E ( trong ba mặt song song,\[x > 0\] ).
Gọi \[y\]là chiều dài mặt hàng rào hình chữ E song song với bờ sông (\[y > 0\]).
Số tiền phải làm là:
\[x.3.50000 + y.60000 = 15.000.000 \Leftrightarrow y = \frac{{500 - 5x}}{2}\].
Diện tích đất:
\[S = x.y = x.\frac{{500 - 5x}}{2} = 250x - \frac{5}{2}{x^2}\]
Ta có:
\[S' = 250 - 5x\].
\[S' = 0 \Leftrightarrow 250 - 5x \Leftrightarrow x = 50.\]
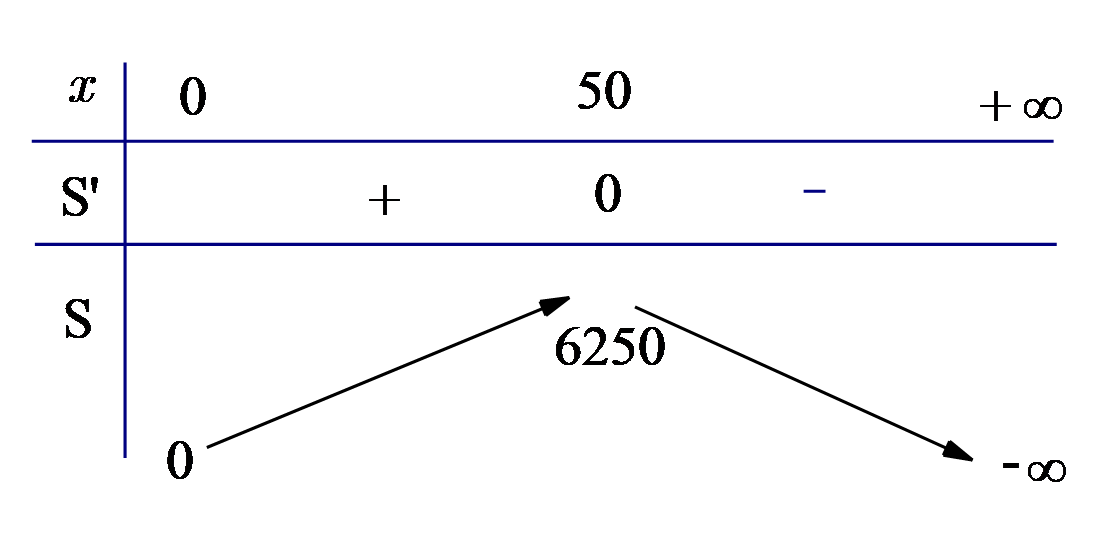
Bảng biến thiên:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tập xác định \(D = \mathbb{R}\).
Đặt \(t = {\cos ^2}x,\) \(t \in \left[ {0\,;\,1} \right]\).
Hàm số viết lại \(y = {t^2} - t + 4\)
\(y' = 2t - 1\)
\(y' = 0 \Leftrightarrow t = \frac{1}{2}\)
Ta có \(y\left( 0 \right) = 4,\) \(y\left( 1 \right) = 4,\) \(y\left( {\frac{1}{2}} \right) = \frac{{15}}{4}\).
Vậy giá trị lớn nhất là 4.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có \(y' = \frac{{2x}}{{\left( {{x^2} + 4} \right)\ln 2}} = 0 \Rightarrow x = 0\).
Khi đó: \(y\left( { - 2} \right) = {\log _2}8 = 3;\,\,\,y\left( 0 \right) = {\log _2}4 = 2;\,\,\,y\left( 5 \right) = {\log _2}29\).
Vậy giá trị lớn nhất của hàm số trên đoạn \[\left[ { - 2;\,5} \right]\] là \({\log _2}29\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập