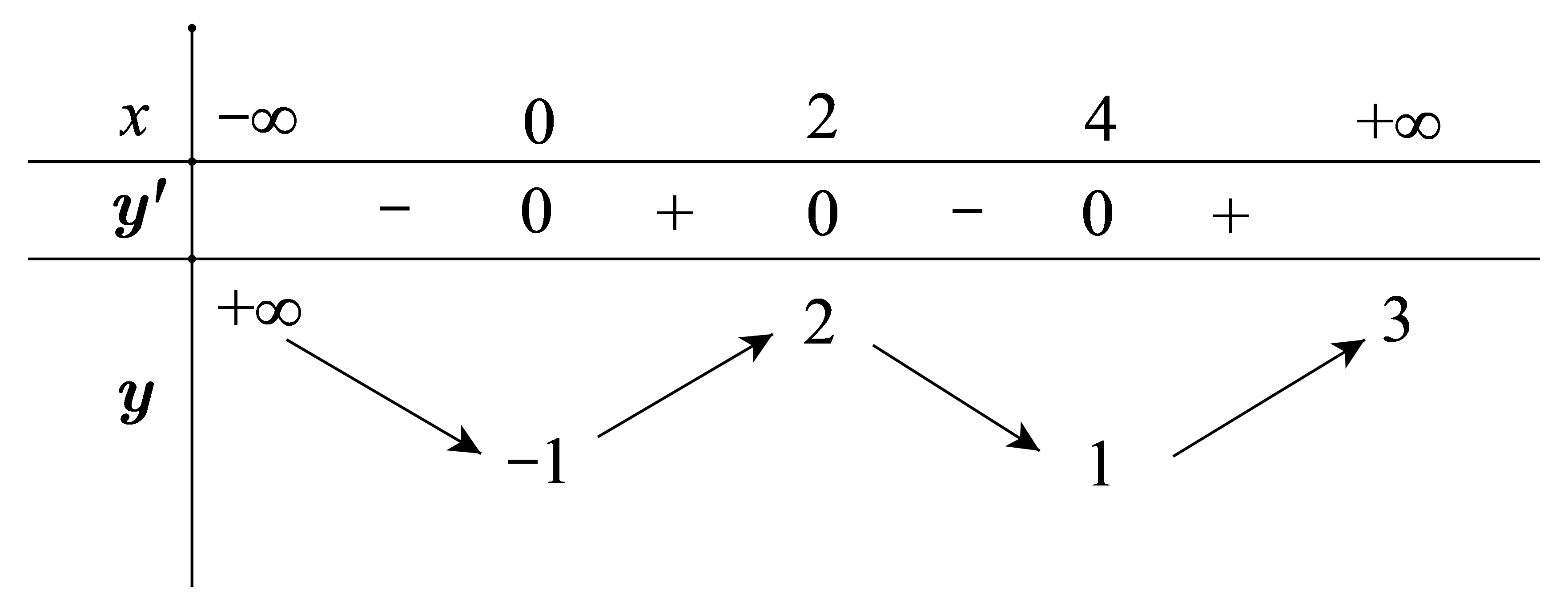Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải) - Đề 2
49 người thi tuần này 4.6 1 K lượt thi 21 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
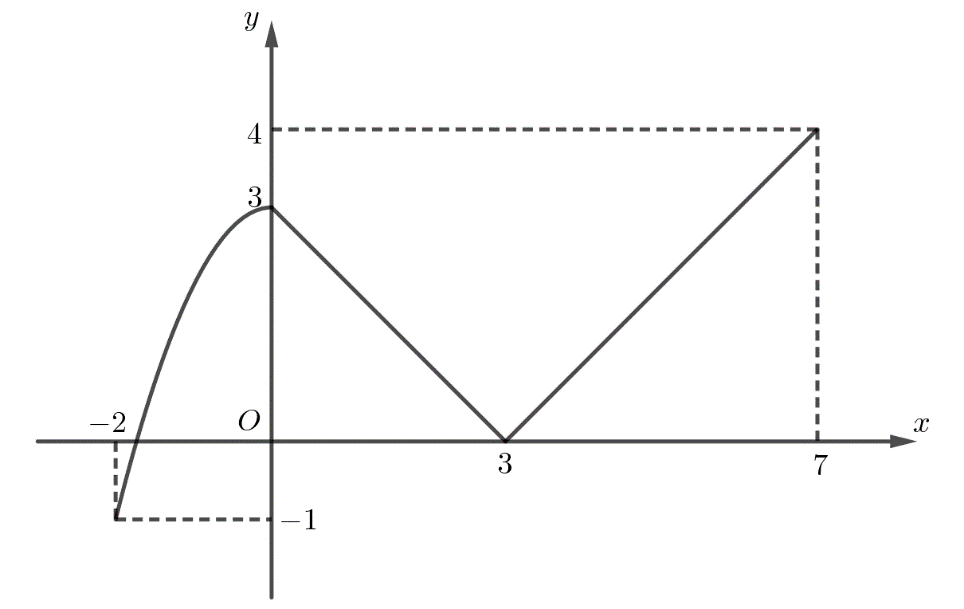
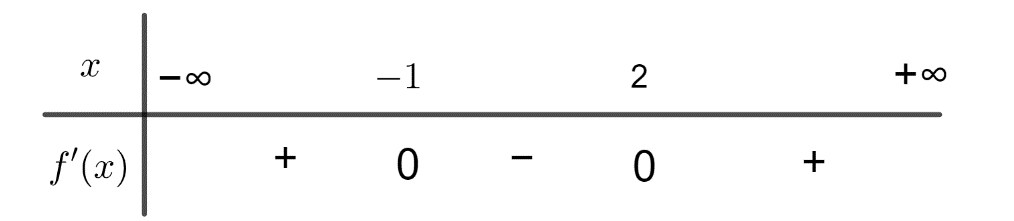
Dựa vào định nghĩa về GTLN và GTNN của hàm số, ta được khẳng định đúng là khẳng định (II).
Câu 2
Lời giải
Ta có: \(y = - {x^2} + 9 \le 9\); \(\forall x \in \mathbb{R}\) nên hàm số đạt giá trị lớn nhất là \(9\).
Lời giải
Câu 4
Lời giải
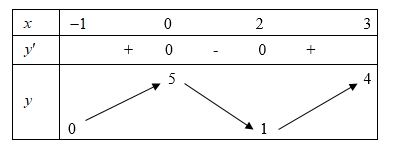
Nhìn vào bảng biến thiên ta thấy \(\mathop {\max }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 0 \right).\)
Câu 5
Lời giải
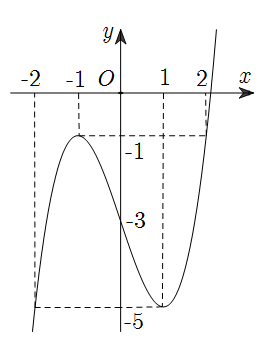
\(M = \mathop {\max }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 1\) khi \(x = - 1\) hoặc \(x = 2\).
\(m = \mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 5\) khi \(x = - 2\) hoặc \(x = 1\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
PHẦN II. Câu trắc nghiệm đúng sai
Cho hàm số \(y = f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\), với \(m\) là tham số.
a) [1] Nếu đồ thị của hàm số \(y = {x^3} - 3{x^2} + m\) luôn cắt trục hoành thì giá trị nhỏ nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) bằng 0.
b) [2] Với \(m = 2\), giá trị nhỏ nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) trên đoạn \(\left[ {3;\,\,5} \right]\) bằng 2.
c) [2] Với \(m < 0\), giá trị lớn nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) trên đoạn \(\left[ {0;\,\,1} \right]\)bằng \(m\).
d) [3] Biết hàm số \(y = f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\) có giá trị nhỏ nhất trên đoạn \(\left[ { - 2;\,\,2} \right]\) bằng 10. Khi đó tổng các giá trị của tham số \(m\) là \(30\).
Cho hàm số \(y = f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\), với \(m\) là tham số.
a) [1] Nếu đồ thị của hàm số \(y = {x^3} - 3{x^2} + m\) luôn cắt trục hoành thì giá trị nhỏ nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) bằng 0.
b) [2] Với \(m = 2\), giá trị nhỏ nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) trên đoạn \(\left[ {3;\,\,5} \right]\) bằng 2.
c) [2] Với \(m < 0\), giá trị lớn nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) trên đoạn \(\left[ {0;\,\,1} \right]\)bằng \(m\).
d) [3] Biết hàm số \(y = f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\) có giá trị nhỏ nhất trên đoạn \(\left[ { - 2;\,\,2} \right]\) bằng 10. Khi đó tổng các giá trị của tham số \(m\) là \(30\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.