Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải)

Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải) - Đề 4

60 người thi tuần này 4.6 737 lượt thi 22 câu hỏi 45 phút

Câu 1

PHÀN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số $y = f\left( x \right)$ liên tục trên đoạn \[\left[ { - 1;3} \right]\] và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số đã cho trên đoạn \[\left[ { - 1;2} \right]\] bằng

A. \[3\].

B. 1.

C. \[ - 2\].

D.\[2\].

Lời giải

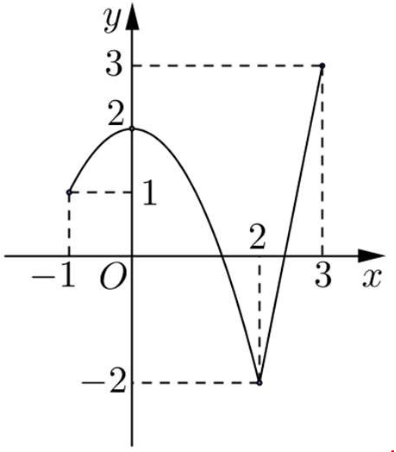
Dựa vào đồ thị ta có $\mathop {max}\limits_{{\rm{[}} - 1;2]} y = 2$

Câu 2

Cho hàm số $y = f\left( x \right)$ liên tục trên $\left[ { - 3;2} \right]$ và có bảng biến thiên như hình dưới đây. Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f\left( x \right)$ trên $\left[ { - 1;2} \right]$. Giá trị của $M + m$ bằng bao nhiêu ?

$Cho hàm số $y = f\left( x \right)$ liên tục trên $\left[ { - 3;2} \right]$ và có bảng biến thiên như hình dưới đây. Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f\left( x \right)$ trên \(\left[ { - 1;2} \righ (ảnh 1)$

A. $3$.

B. $2$.

C. $1$.

D. $4$.

Lời giải

Ta có \[M = \mathop {max}\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) = 3\] và $m = \mathop {min}\limits_{\left[ { - 1;2} \right]} \,f\left( x \right) = f\left( 0 \right) = 0$.

Vậy $M + m = 3$.

Câu 3

Gọi \[m\] là giá trị nhỏ nhất của hàm số $y = \frac{{{x^2} + 3}}{{x - 1}}$ trên đoạn $\left[ {2;4} \right]$. Khi đó:

A. $m = 6$.

B. $m = - 2$.

C. $m = - 3$.

D. $m = \frac{{19}}{3}$.

Lời giải

Chọn A.

Hàm số $y = \frac{{{x^2} + 3}}{{x - 1}}$ liên tục trên đoạn $\left[ {2;4} \right].$

Ta có $y'\left( x \right) = \frac{{{x^2} - 2x - 3}}{{{{\left( {x - 1} \right)}^2}}} \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \notin \left( {2;\,4} \right)\\x = 3\,\,\,\, \in \left( {2;\,4} \right)\end{array} \right.$

Tính $y'\left( 2 \right) = 7;\,\,y'\left( 4 \right) = \frac{{19}}{3};\,\,y'\left( 3 \right) = 6$.

Suy ra $m = 6$.

Sử dụng Casio

Nhập MODE 7 . $f\left( X \right) = \frac{{{x^2} + 3}}{{x - 1}}$.

Start? $2$ End? $4$ Step? $\frac{1}{9}$. Kết luận.

Câu 4

Tìm giá trị nhỏ nhất của hàm số \[y = f\left( x \right) = {x^2} - 3x\] trên đoạn $\left[ {0;2} \right].$

A. \[ - \frac{9}{4}\].

B. \[ - \frac{3}{2}\].

C. \[0\].

D. \[5\].

Lời giải

Chọn A

\[f'(x) = 2x - 3\]

\[f'(x) = 0 \Rightarrow 2x - 3 = 0 \Leftrightarrow x = \frac{3}{2}\]

\[f(0) = 0;f(2) = - 2;f\left( {\frac{3}{2}} \right) = \frac{{ - 9}}{4}\]

Vậy giá trị nhỏ nhất của hàm số là \[\frac{{ - 9}}{4}\] khi \[x = \frac{3}{2}\]

Câu 5

Cho hàm số \[y = f\left( x \right)\] xác định, liên tục trên đoạn \[\left[ { - 2\,;\,2} \right]\] và có đồ thị là đường cong trong hình vẽ sau:

Tìm khẳng định đúng trong các khẳng định sau:

A. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 4\].

B. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = 1\].

C. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = 2\].

D. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 2\].

Lời giải

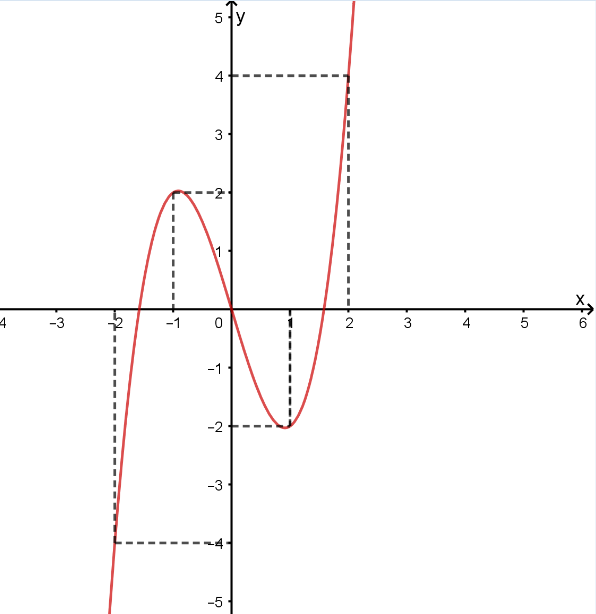
Quan sát đồ thị trên đoạn \[\left[ { - 2\,;\,2} \right]\], giá trị nhỏ nhất của hàm số \[y = f\left( x \right)\] là \[ - 4\].

Câu 6

Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

$Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau: Giá trị lớn nhất của hàm số $y = f\left( x \right)$trên đoạn $\left[ {0;2} \right]$ bằng A. $1$. B. $3$. C. $0$. D. $2$. (ảnh 1)$
Giá trị lớn nhất của hàm số $y = f\left( x \right)$trên đoạn $\left[ {0;2} \right]$ bằng

A. $1$.

B. $3$.

C. $0$.

D. $2$.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Bright

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý