Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá \(30.000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \(30.000\) đồng mà cứ tăng giá thêm \(1000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18.000\).
a) Nếu cơ sở bán mỗi chiếc khăn với giá \(37000\)(đồng) thì số tiền lãi sau 1 tháng là \(44\)(triệu đồng).
b) Sau khi cơ sở tăng giá mỗi chiếc khăn thêm \(x\) (nghìn đồng) thì tổng số lợi nhuận một tháng của cơ sở được tính theo công thức\(f\left( x \right) = - 100{x^2} + 1800x + 36000\).
c) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm \[800\] chiếc.
d) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá \[39000\] đồng.
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá \(30.000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \(30.000\) đồng mà cứ tăng giá thêm \(1000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18.000\).
a) Nếu cơ sở bán mỗi chiếc khăn với giá \(37000\)(đồng) thì số tiền lãi sau 1 tháng là \(44\)(triệu đồng).
b) Sau khi cơ sở tăng giá mỗi chiếc khăn thêm \(x\) (nghìn đồng) thì tổng số lợi nhuận một tháng của cơ sở được tính theo công thức\(f\left( x \right) = - 100{x^2} + 1800x + 36000\).
c) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm \[800\] chiếc.
d) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá \[39000\] đồng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số tiền cần tăng giá mỗi chiếc khăn là \(x\) (nghìn đồng).
Vì cứ tăng giá thêm \(1\) (nghìn đồng) thì số khăn bán ra giảm \(100\) chiếc nên tăng \(x\) (nghìn đồng) thì số khăn bán ra giảm \(100x\) chiếc.
Do đó tổng số khăn bán ra mỗi tháng là: \(3000 - 100x\) chiếc.
Lúc đầu bán với giá \(30\) (nghìn đồng), mỗi chiếc khăn có lãi \(12\) (nghìn đồng). Sau khi tăng giá, mỗi chiếc khăn thu được số lãi là: \(12 + x\) (nghìn đồng).
Do đó tổng số lợi nhuận một tháng thu được sau khi tăng giá là:
\(f\left( x \right) = \left( {3000 - 100x} \right)\left( {12 + x} \right)\) (nghìn đồng).
Xét hàm số \(f\left( x \right) = \left( {3000 - 100x} \right)\left( {12 + x} \right)\) trên \(\left( {0; + \infty } \right)\).
Ta có: \(f\left( x \right) = - 100{x^2} + 1800x + 36000\).
\(f'\left( x \right) = - 200x + 1800\)
\(f'\left( x \right) = 0 \Leftrightarrow - 200x + 1800 = 0 \Leftrightarrow x = 9\)
Lập bảng biến thiên của hàm số \(f\left( x \right)\) trên \(\left( {0;\, + \infty } \right)\) ta thấy hàm số đạt giá trị lớn nhất khi\[x = 9\]
Như vậy, để thu được lợi nhuận cao nhất thì cơ sở sản xuất cần tăng giá bán mỗi chiếc khăn là \(9.000\) đồng, tức là mỗi chiếc khăn bán với giá mới là\(39.000\) đồng.
Vậy:
a) sai.
b) đúng.
c) sai.
d) đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Dựa vào đồ thị ta có \(\mathop {max}\limits_{{\rm{[}} - 1;2]} y = 2\)
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn C
\[f\left( x \right) = - \frac{1}{{40}}{x^3} + \frac{3}{4}{x^2}\]
\[f'\left( x \right) = - \frac{3}{{40}}{x^2} + \frac{3}{2}x\]
\[f'\left( x \right) = 0 \Leftrightarrow - \frac{3}{{40}}{x^2} + \frac{3}{2}x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0(l)\\x = 20(n)\end{array} \right.\]
Bảng biến thiên.
![Tìm giá trị lớn nhất của hàm số \[f\left( x \right) = \frac{1}{{40}}{x^2}\left( {30 - x} \right)\] trên nửa khoảng \[\left( {0; + \infty } \right)\] A. \[20\]. B. \[24\]. C. \[25\]. D. \[30\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/5-1759148881.png)
Vậy giá trị lớn nhất của hàm số là \[25\] khi \[x = 20\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
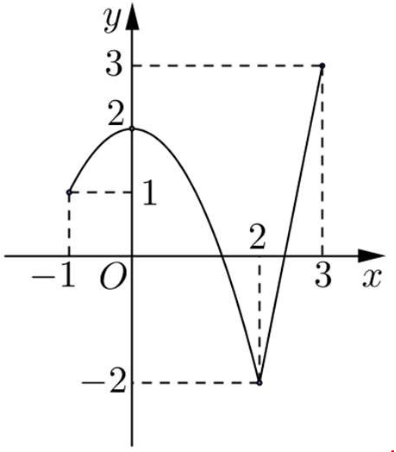
![Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759149338.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập