Anh Hà dự định làm một cái thùng đựng dầu hình trụ bằng sắt có nắp đậy thể tích \(10\,{m^3}\). Chi phí làm mỗi \({m^2}\) đáy là 400 ngàn đồng, mỗi \({m^2}\) nắp là 200 ngàn đồng, mỗi \({m^2}\) mặt xung quanh là 300 ngàn đồng. Để chi phí làm thùng là ít nhất thì anh Hà cần chọn chiều cao của thùng là……………………….. (Xem độ dày của tấm sắt làm thùng là không đáng kể, làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp số: \(2,34\)
Gọi bán kính đáy của hình trụ là \(R,R > 0\). Ta có
\(V = \pi {R^2}h \Rightarrow h = \frac{{10}}{{\pi {R^2}}}\).
Suy ra chi phí (đơn vị ngàn đồng) làm thùng
\(\begin{array}{l}C = \pi {R^2}.400 + \pi {R^2}.200 + 2\pi Rh.300\\\,\,\,\,\, = 600\left( {\pi {R^2} + \frac{{10}}{R}} \right)\end{array}\).
\(C' = 600\left( {2\pi R - \frac{{10}}{{{R^2}}}} \right)\); \(C' = 0 \Leftrightarrow 2\pi R - \frac{{10}}{{{R^2}}} = 0 \Leftrightarrow {R^3} = \frac{5}{\pi } \Leftrightarrow R = \sqrt[3]{{\frac{5}{\pi }}}\)
Bảng biến thiên
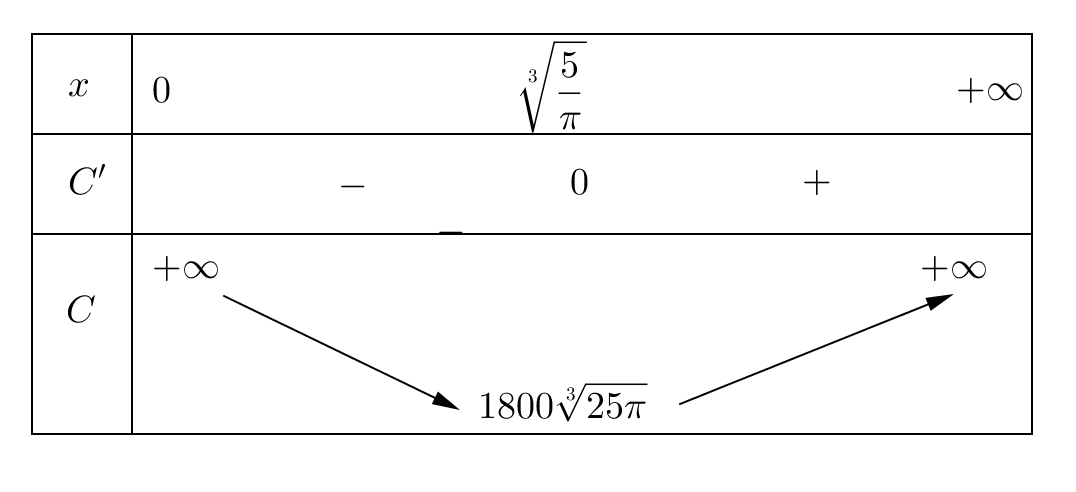
Dẫn dến
\(\mathop {\min }\limits_{\left( {0; + \infty } \right)} C = 1800\sqrt[3]{{25\pi }} \Leftrightarrow R = \sqrt[3]{{\frac{5}{\pi }}}\).
Vậy để chi phí nhỏ nhất thì chiều cao của hình trụ là \(h = \frac{{10}}{{\sqrt[3]{{25\pi }}}} \approx 2,34\,m\).
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: \(0,37\)
- Hàm số \(g(x) = \frac{{\ln x}}{x}\) liên tục trên đoạn \([1;4]\)
Ta có: \({g^\prime }(x) = \frac{{1 - \ln x}}{{{x^2}}}\). Khi đó, trên khoảng \((1;4),{g^\prime }(x) = 0\) khi \(x = e\).
\(g(1) = 0,g(e) = \frac{1}{e},g(4) = \frac{{\ln 4}}{4} = \frac{{\ln 2}}{2}\).
Vậy \(\mathop {\max }\limits_{\left[ {1;4} \right]} g(x) = \frac{1}{e},\mathop {\min }\limits_{\left[ {1;4} \right]} g(x) = 0 \Rightarrow \mathop {\max }\limits_{\left[ {1;4} \right]} g(x) + \mathop {\min }\limits_{\left[ {1;4} \right]} g(x) = \frac{1}{e} \approx 0,37\).
Câu 2
A. \[3\].
B. 1.
C. \[ - 2\].
D.\[2\].
Lời giải
Dựa vào đồ thị ta có \(\mathop {max}\limits_{{\rm{[}} - 1;2]} y = 2\)
Câu 3
A. \(e - \ln 2 - \frac{1}{2}\).
B. \(e - 1\).
C. \(\ln 2 - \frac{1}{2}\).
D. \(e - 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
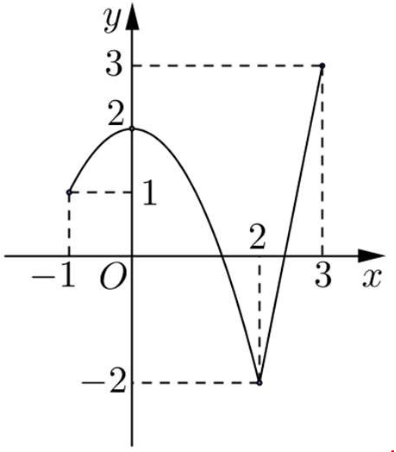
![Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759149338.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo