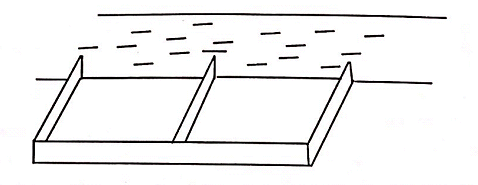
Từ hình vuông có cạnh bằng \[6\] người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó người ta gập thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi cạnh hình tam giác cân bị cắt bỏ có độ dài \(x\,\,(0 < x < 3)\)
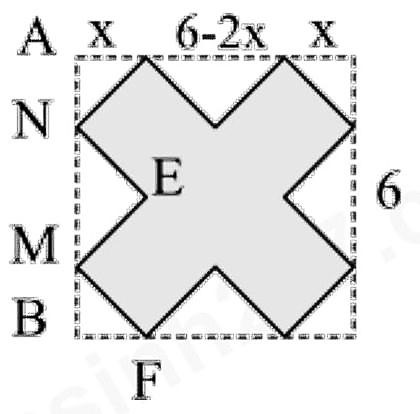
\( \Rightarrow AN = BM = x \Rightarrow MN = 6 - 2x\)
\( \Rightarrow EM = EN = \frac{{6 - 2x}}{{\sqrt 2 }}\)
Hình hộp chữ nhật có đáy là hình vuông cạnh \(MF = x\sqrt 2 \),
Có chiều cao \(EN = \frac{{6 - 2x}}{{\sqrt 2 }}\)
\( \Rightarrow V = M{F^2}.EN = 2{x^2}.\frac{{6 - 2x}}{{\sqrt 2 }} = \sqrt 2 {x^2}\left( {6 - 2x} \right) = - 2\sqrt 2 {x^3} + 6\sqrt 2 {x^2}\)
\( \Rightarrow V' = - 6\sqrt 2 {x^2} + 12\sqrt 2 x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\end{array}} \right.\)
\( \Rightarrow {V_{{\rm{max}}}} = V\left( 2 \right) = - 2\sqrt 2 {.2^3} + 6\sqrt 2 {.2^2} = 8\sqrt 2 \)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tập xác định \(D = \mathbb{R}\).
Đặt \(t = {\cos ^2}x,\) \(t \in \left[ {0\,;\,1} \right]\).
Hàm số viết lại \(y = {t^2} - t + 4\)
\(y' = 2t - 1\)
\(y' = 0 \Leftrightarrow t = \frac{1}{2}\)
Ta có \(y\left( 0 \right) = 4,\) \(y\left( 1 \right) = 4,\) \(y\left( {\frac{1}{2}} \right) = \frac{{15}}{4}\).
Vậy giá trị lớn nhất là 4.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có \(y' = \frac{{2x}}{{\left( {{x^2} + 4} \right)\ln 2}} = 0 \Rightarrow x = 0\).
Khi đó: \(y\left( { - 2} \right) = {\log _2}8 = 3;\,\,\,y\left( 0 \right) = {\log _2}4 = 2;\,\,\,y\left( 5 \right) = {\log _2}29\).
Vậy giá trị lớn nhất của hàm số trên đoạn \[\left[ { - 2;\,5} \right]\] là \({\log _2}29\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập