Gọi S là tập hợp chứa các tham số \(m\) để đồ thị hàm số \(y = \frac{{mx - 1}}{{x + m}}\) có tiệm cận đứng và tiệm cận ngang tạo với các trục tọa độ hình chữ nhật có diện tích bằng 4. Số phần tử của S là
Quảng cáo
Trả lời:
Đáp án: 2.
Phương trình tiệm cận ngang là \(y = m\)
Phương trình tiệm cận đứng là \(x = - m\)
Theo đề bài ta có: \(\left| m \right|\left| { - m} \right| = 4 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\)
Vậy S có 2 phần tử.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0.
Nhìn vào bảng biến thiên ta thấy \(\mathop {\max }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = 5 = f\left( 0 \right).\) Vậy giá trị lớn nhất của \(y = f(x)\)trên \(\left[ { - 1\,;\,3} \right]\)đạt được tại \({x_0} = 0\).
Câu 2
Lời giải
Xét hàm số \(f\left( x \right) = \frac{{{x^2} + 4}}{x},\,\forall x \in \left( {0; + \infty } \right)\)
Ta có \(f'\left( x \right) = \frac{{{x^2} - 4}}{{{x^2}}}\). Khi đó \(f'\left( x \right) = 0,x \in \left( {0; + \infty } \right) \Leftrightarrow x = 2\).
Ngoài ra: \(\mathop {\lim }\limits_{x \to {0^ + }} = + \infty ,\,\mathop {\lim }\limits_{x \to + \infty } = + \infty \)
Ta có bảng biến thiên hàm số như sau:
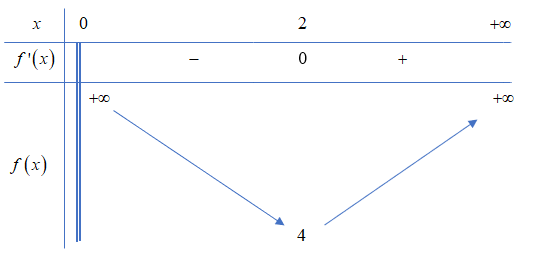
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \(y = f(x)\) liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1\,;\,3} \right]\) như hình vẽ bên. Giả sử giá trị lớn nhất của \(y = f(x)\)trên \(\left[ { - 1\,;\,3} \right]\)đạt được tại giá trị x0. Tìm x0 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759150879.png)
![Đặt \[g\left( x \right) = \left| {f\left( {{x^2}} \right) + m} \right|\]. Có bao nhiêu giá trị nguyên thuộc [-2024;2024] của tham số m để với mọi bộ ba số phân biệt (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/10-1759151329.png)
![Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên R, có đồ thị trên đoạn\(\left[ { - 1;\,3} \right]\) như hình vẽ dưới đây. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/21-1759150014.png)
![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1\,;\,3} \right]\) và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 1\,;\,3} \right]\) bằng A. \[3\]. B. \[2\]. C. \[0\]. D. \[1\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759149666.png)
![Giả sử giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của \(f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\)đạt được lần lượt tại \({x_0}\)và\({x_1}\). Tìm\({x_0}\)và\({x_1}\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/screenshot-3628-1759151183.png)