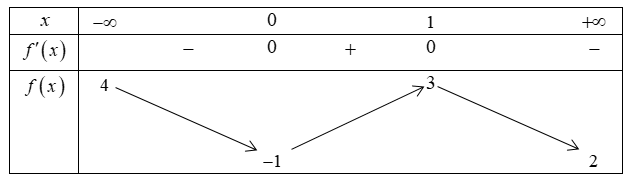
Cho hàm số \(y = \frac{{x - 1}}{{m{x^2} - 2x + 3}}\) \[\left( C \right)\].
a) Khi \(m \ne 0\), hàm số có tiệm cận ngang \(y = 0\).
b) Khi \(m = 0\), tọa độ giao điểm của hai đường tiệm cận thuộc đường thẳng \(x - y - 2 = 0\).
c) Hàm số có 1 tiệm cận đứng khi \(m = 2\)
d) Gọi S là tập hợp các giá trị nguyên âm của \(m \in \left[ { - 5; - 1} \right]\) để hàm số có ba đường tiệm cận. Số phần tử của S là 1.
Cho hàm số \(y = \frac{{x - 1}}{{m{x^2} - 2x + 3}}\) \[\left( C \right)\].
a) Khi \(m \ne 0\), hàm số có tiệm cận ngang \(y = 0\).
b) Khi \(m = 0\), tọa độ giao điểm của hai đường tiệm cận thuộc đường thẳng \(x - y - 2 = 0\).
c) Hàm số có 1 tiệm cận đứng khi \(m = 2\)
d) Gọi S là tập hợp các giá trị nguyên âm của \(m \in \left[ { - 5; - 1} \right]\) để hàm số có ba đường tiệm cận. Số phần tử của S là 1.
Câu hỏi trong đề: Đề kiểm tra Đường tiệm cận của đồ thị hàm số (có lời giải) !!
Quảng cáo
Trả lời:
a) Đúng
Khi \(m \ne 0\)
Vì \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x - 1}}{{m{x^2} - 2x + 3}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{x} - \frac{1}{{{x^2}}}}}{{m - \frac{2}{x} + \frac{3}{{{x^2}}}}} = 0\) nên hàm số có tiệm cận ngang \(y = 0\).
b) Đúng.
Khi \(m = 0\) hàm số có dạng \(y = \frac{{x - 1}}{{ - 2x + 3}}\)
Hàm số có 1 tiệm cận đứng là \(x = \frac{3}{2}\) và 1 tiệm cận ngang là \(y = - \frac{1}{2}\), nên tọa độ giao điểm hai đường tiệm cận là \(I\left( {\frac{3}{2}; - \frac{1}{2}} \right)\). Rõ ràng I thuộc đường thẳng \(x - y - 2 = 0\).
c) Sai.
Khi \(m = 2\) thì hàm số thành \(y = \frac{{x - 1}}{{2{x^2} - 2x + 3}}\) không có tiệm cận đứng vì \(2{x^2} - 2x + 3 = 0\) vô nghiệm
d) Sai.
Đồ thị hàm số có ba đường tiệm cận Û \(m{x^2} - 2x + 3 = 0\) có hai nghiệm phân biệt khác 1.
\( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\\m{.1^2} - 2.1 + 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m < \frac{1}{3}\\m \ne - 1\end{array} \right.\).
Vì \(m \in \left[ { - 5; - 1} \right]\) nên \(S = \left\{ { - 5; - 4; - 3; - 2} \right\}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chi phí sản xuất trung bình cho mỗi sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{150x + 900}}{x}\).
Ta có \(f'\left( x \right) = \frac{{ - 900}}{{{x^2}}} < 0\,\forall x > 0\).
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{150x + 900}}{x} = 150\).
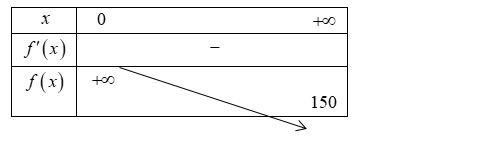
Vậy khi sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình cho mỗi sản phẩm càng giảm, nhưng không dưới \(150\) nghìn đồng.
Đáp án: \(150\)
Câu 2
Lời giải
Chọn C
Theo định nghĩa của tiệm cận xiên.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.