Giả sử chi phí cho xuất bản \(x\) cuốn tạp chí (gồm: lương cán bộ, công nhân viên, giấy in,...) được cho bởi công thức:
\(C(x) = 0,0001{x^2} - 0,2x + 10000,\)
trong đó \(C(x)\) được tính theo đơn vị là vạn đồng (1 vạn đồng \( = \) 10000 đồng). Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số \(M(x) = \frac{{T(x)}}{x}\) được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản \(x\) cuốn và tổng chi phí \(T(x)\) (xuất bản và phát hành) cho \(x\) cuốn tạp chí. Tìm chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá 30000 cuốn?
Giả sử chi phí cho xuất bản \(x\) cuốn tạp chí (gồm: lương cán bộ, công nhân viên, giấy in,...) được cho bởi công thức:
\(C(x) = 0,0001{x^2} - 0,2x + 10000,\)
trong đó \(C(x)\) được tính theo đơn vị là vạn đồng (1 vạn đồng \( = \) 10000 đồng). Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số \(M(x) = \frac{{T(x)}}{x}\) được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản \(x\) cuốn và tổng chi phí \(T(x)\) (xuất bản và phát hành) cho \(x\) cuốn tạp chí. Tìm chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá 30000 cuốn?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 2,2
Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng, tức là 0,4 vạn đồng.
Suy ra chi phí phát hành cho \(x\) cuốn là \(0,4x\)(vạn đồng).
Theo đề bài, ta có tổng chi phí xuất bản và phát hành cho \(x\) cuốn tạp chí là:
\(T\left( x \right) = C\left( x \right) + 0,4x = 0,0001{x^2} + 0,2x + 10000,\)với \(x > 0.\)
Ta có \(f\left( x \right) = M(x) = \frac{{T(x)}}{x} = 0,0001x + 0,2 + \frac{{10000}}{x}\).
Xét hàm số \(f(x) = 0,0001x + 0,2 + \frac{{10000}}{x}\), với \(0 < x \le 30000\).
\(\begin{array}{l}f'\left( x \right) = 0,0001 - \frac{{10000}}{{{x^2}}} = \frac{{0,0001{x^2} - 10000}}{{{x^2}}};\\f'\left( x \right) = 0 \Leftrightarrow x = 10000\,\,\left( {{\rm{do }}x > 0} \right).\\\mathop {\lim }\limits_{x \to {0^ + }} f(x) = + \infty .\end{array}\)
Bảng biến thiên:
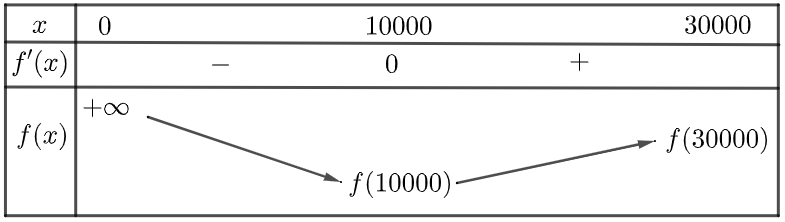
Dựa vào bảng biến thiên, ta thấy giá trị của \(M(x)\) nhỏ nhất khi \(x = 10000\).
Do đó, số lượng tạp chí cần xuất bản sao cho chi phí trung bình thấp nhất là \(x = 10000\) (cuốn).
Vậy chi phí trung bình cho một cuốn tạp chí khi xuất bản 10000 cuốn là:\(M(10000) = 2,2\) (vạn đồng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 32,6
Để nồng độ chất độc trong máu thấp nhất khi thời gian di chuyển về đến tại thấp nhất.
Vậy nên Quãng đường ông Vinh di chuyển về đến trại phải thấp nhất.
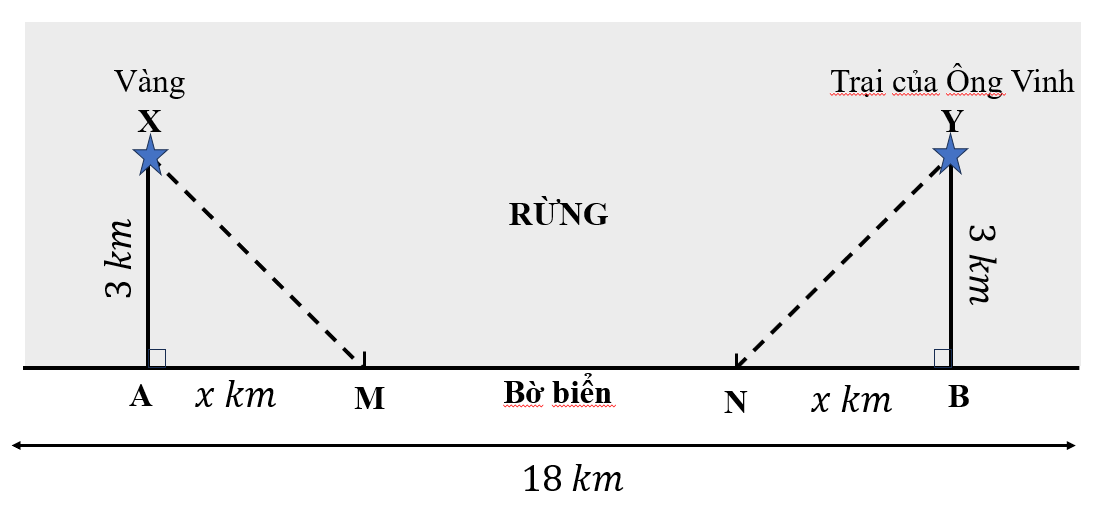
Quãng đường của Ông Vinh
Theo bài ra ta có: ông Vinh sẽ đi qua các quãng đường \[XM + MN + NY.\]
Ta có: \[XM = NY = \sqrt {9 + {x^2}} \]; \[MN = 18 - 2x\]
Thời gian Ông Vinh chạy đến Trại nghỉ là: \[T(x) = 2\left( {\frac{{\sqrt {9 + {x^2}} }}{5} + \frac{{9 - x}}{{13}}} \right)\] với \[x \in \left( {0;9} \right)\]
Xét \[T'(x) = 2\left( {\frac{{\sqrt {9 + {x^2}} }}{5} + \frac{{9 - x}}{{13}}} \right) = 0 \Leftrightarrow x = \frac{5}{4}\] ( thỏa mãn)
Bảng biến thiên:
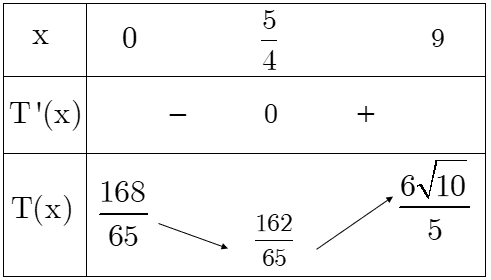
Dựa vào bảng biến thiên, ta thấy giá trị của \(T(x)\) nhỏ nhất khi \(x = \frac{5}{4}\).
\[ \Rightarrow \mathop {Min}\limits_{x \in \left( {0,9} \right)} {\rm{ }}T(x) = T(\frac{5}{4}) = \frac{{162}}{{65}}\]
Vậy, nồng độ chất độc trong máu thấp nhất là \[\mathop {\min }\limits_{(0, + \infty )} y = 50\log \left( {\frac{{162}}{{65}} + 2} \right) \approx 32,6\]
![Hai cột đỡ dọc \[MN\] và \[PQ\] ( song song với trục \[Oy\]) là đoạn nối giữa khung của Parabol và đường \[XY\]. Tính tổng độ d (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759200516.png)
Lời giải
Đáp án: 49,5
Theo bài ra ta có: phương trình của Parabol là \[y = 60 - \frac{3}{{80}}{x^2}\].
Khoảng cách giữa khung Parabol và đường xuyên núi là:
\[D = 60 - \frac{3}{{80}}{x^2} - \left( {\frac{{{x^3}}}{{25600}} - \frac{{3x}}{{16}} + 35} \right)\] với \[x \in \left( { - 23,71;27,99} \right)\]
Xét \[D' = - \frac{3}{{40}}x - \frac{{3{x^2}}}{{25600}} + \frac{3}{{16}} = 0 \Leftrightarrow x = 2,49\]
Bảng biến thiên:
![Hai cột đỡ dọc \[MN\] và \[PQ\] ( song song với trục \[Oy\]) là đoạn nối giữa khung của Parabol và đường \[XY\]. Tính tổng độ d (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759200546.png)
Dựa vào bảng biến thiên, \[MN\] là đoạn có độ dài lớn nhất khi \[x = 2,49\]\[ \Rightarrow MN = {D_{MN}} = 60 - \frac{3}{{80}}.2,{49^2} - \left( {\frac{{2,{{49}^3}}}{{25600}} - \frac{{3.2,49}}{{16}} + 35} \right) \approx 25,23\]
Vì \[N\]và \[Q\] là hai điểm đối xứng qua \[Oy\]\[ \Rightarrow {x_{PQ}} \approx - 2,49\]
\[ \Rightarrow PQ = {D_{PQ}} = 60 - \frac{3}{{80}}.2,{49^2} - \left( {\frac{{ - 2,{{49}^3}}}{{25600}} - \frac{{3. - 2,49}}{{16}} + 35} \right) \approx 24,3\]
Tổng độ dài \[MN + PQ = 49,5\].
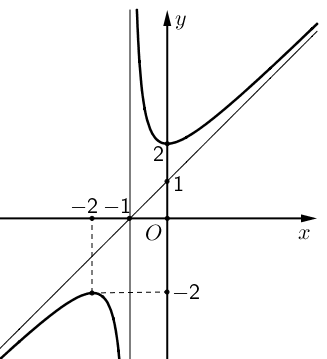
![Cho hàm số hữu tỉ \[y = ax + 2 + \frac{b}{{x + c}}\] có đồ thị như hình bên dưới. Tính\(P = a + b + c.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/12-1759200440.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(y = x + 2\).
B. \(y = x + 4\).
C. \(y = x - 3\).
D. \(y = x - 5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập