Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
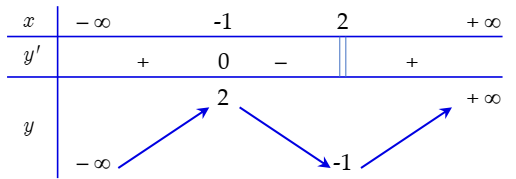 Mệnh đề nào dưới đây là sai?
Mệnh đề nào dưới đây là sai?

Câu hỏi trong đề: Đề kiểm tra Toán 12 Chân trời sáng tạo Chương 1 có đáp án !!
Quảng cáo
Trả lời:
Chọn A
Dựa vào BBT ta thấy hàm số đạt cực tiểu tại \(x = 2\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
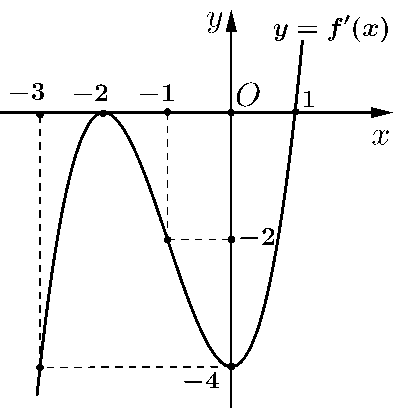
a) Sai. Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) \ge 0\) với \(\forall x \ge 1\) nên hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
b) Sai. Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\) chỉ đổi dấu một lần qua \(x = 1\) nên hàm số có một điểm cực trị.
c) Sai. Từ đồ thị ta có hàm số \(f'\left( x \right)\) có dạng: \(f'\left( x \right) = a{\left( {x + 2} \right)^2}\left( {x - 1} \right)\).
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua \(\left( {0; - 4} \right)\) nên: \( - 4 = a{\left( {0 + 2} \right)^2}\left( {0 - 1} \right) \Leftrightarrow a = 1\).
Vậy \(f'\left( x \right) = {\left( {x + 2} \right)^2}\left( {x - 1} \right) \Rightarrow f'\left( 2 \right) = {\left( {2 + 2} \right)^2}\left( {2 - 1} \right) = 16\).
d) Đúng. Ta có: \(g'\left( x \right) = f'\left( x \right) - x + 1 = 0 \Leftrightarrow f'\left( x \right) = x - 1\).
Vẽ đường thẳng \(y = x - 1\) trên cùng hệ trục tọa độ với đồ thị hàm số \(y = f'\left( x \right)\).
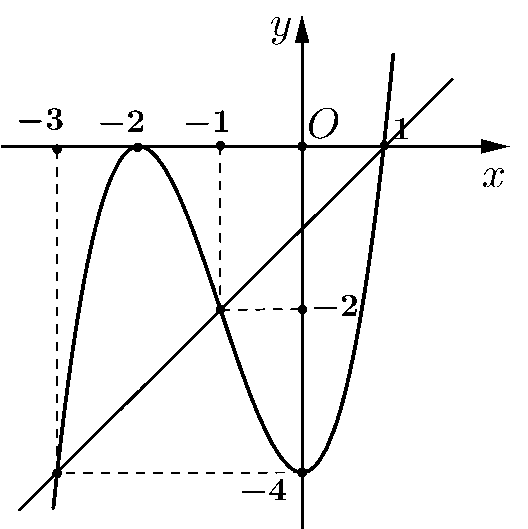
Khi đó: \(f'\left( x \right) = x - 1 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\\x = 1\end{array} \right.\).
Bảng biến thiên của hàm số \(g\left( x \right)\).

Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) nên \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Lời giải
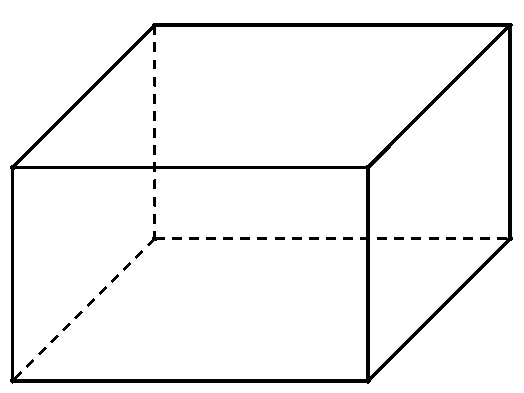
Gọi chiều rộng của bể là \(3x{\rm{ }}\left( {\rm{m}} \right)\). Ta có chiều dài bể là \(4x{\rm{ (m)}}\) và chiều cao của bể là \(\frac{2}{{3{x^2}}}\left( {\rm{m}} \right).\)
Khi đó tổng diện tích bề mặt xây là:
\(T = \left( {3x + 4x} \right).2.\frac{2}{{3{x^2}}} + 2.3x.4x - \frac{2}{9}.3x.4x = \frac{{28}}{{3{x^2}}} + \frac{{64{x^2}}}{3} \ge 2.\sqrt {\frac{{28}}{{3{x^2}}}.\frac{{64{x^2}}}{3}} = \frac{{32\sqrt 7 }}{3}{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Chi phí \(C\) (tính theo đồng) xây dựng là: \(C = T.980000 \ge \frac{{32\sqrt 7 }}{3}.980000 \approx 27657000\) (đồng).
Vậy chi phí thấp nhất mà ông Nam phải chi trả là \(28\) triệu đồng.
Đáp án: 28.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Chọn C Từ đồ thị ta thấy trên đoạn \(\left[ { - 2;2} \right]\) có \(m = - 5,M = - 1\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/2-1759417823.png)