Ông Nam cần xây dựng một bể nước mưa có thể tích \(V = 8\left( {{{\rm{m}}^{\rm{3}}}} \right)\) dạng hình hộp chữ nhật với chiều dài gấp \(\frac{4}{3}\) lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980.000đ/m2 và ở nắp để hở một khoảng hình vuông có diện tích bằng \(\frac{2}{9}\) diện tích nắp bể. Tính chi phí thấp nhất        mà ông Nam phải chi trả (làm tròn đến hàng triệu đồng).

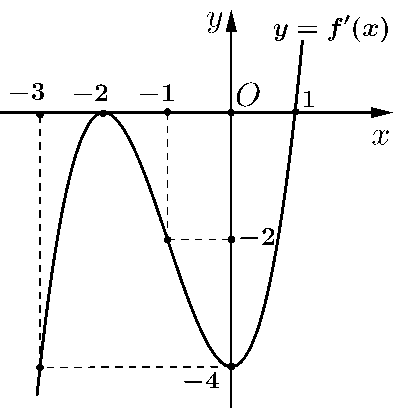
a) Sai. Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) \ge 0\) với \(\forall x \ge 1\) nên hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).

b) Sai. Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\) chỉ đổi dấu một lần qua \(x = 1\) nên hàm số có một điểm cực trị.

c) Sai. Từ đồ thị ta có hàm số \(f'\left( x \right)\) có dạng: \(f'\left( x \right) = a{\left( {x + 2} \right)^2}\left( {x - 1} \right)\).

Đồ thị hàm số \(y = f'\left( x \right)\) đi qua \(\left( {0; - 4} \right)\) nên: \( - 4 = a{\left( {0 + 2} \right)^2}\left( {0 - 1} \right) \Leftrightarrow a = 1\).

Vậy \(f'\left( x \right) = {\left( {x + 2} \right)^2}\left( {x - 1} \right) \Rightarrow f'\left( 2 \right) = {\left( {2 + 2} \right)^2}\left( {2 - 1} \right) = 16\).

d) Đúng. Ta có: \(g'\left( x \right) = f'\left( x \right) - x + 1 = 0 \Leftrightarrow f'\left( x \right) = x - 1\).

Vẽ đường thẳng \(y = x - 1\) trên cùng hệ trục tọa độ với đồ thị hàm số \(y = f'\left( x \right)\).

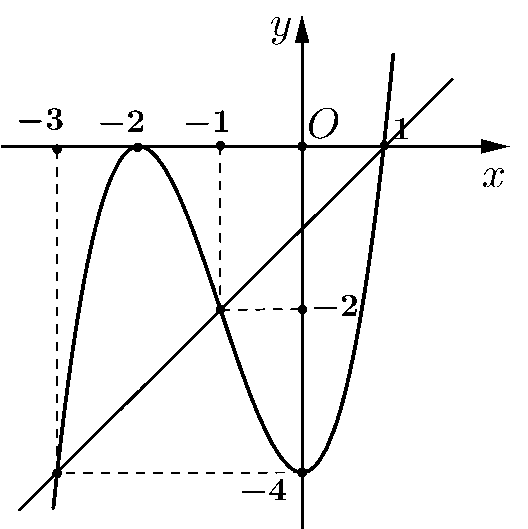
Khi đó: \(f'\left( x \right) = x - 1 \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x =  - 1\\x = 1\end{array} \right.\).

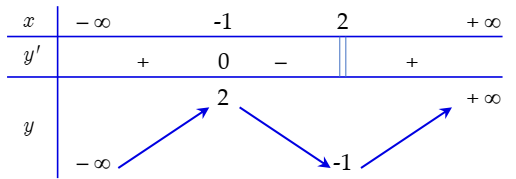
 Bảng biến thiên của hàm số \(g\left( x \right)\).

Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) nên \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).

a) Đúng.

\(h\left( t \right) =  - 0,01{t^3} + 1,1{t^2} - 30t + 250 \Rightarrow h'\left( t \right) =  - 0,03{t^2} + 2,2t - 30 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 55 \notin \left( {0;50} \right)\\t = 18 \in \left( {0;50} \right)\end{array} \right.\)

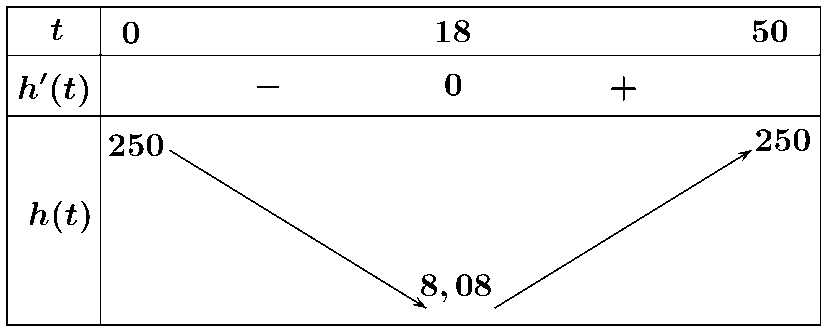
b) Sai. Dựa vào bảng biến thiên trên ta thấy trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao thấp nhất mà con tàu đạt được tại thời điểm \(t \approx 18\left( {\rm{s}} \right)\).

c) Đúng. \(h\left( t \right) =  - 0,01{t^3} + 1,1{t^2} - 30t + 250 \Rightarrow v\left( t \right) = h'\left( t \right) =  - 0,03{t^2} + 2,2t - 30\)

\( \Rightarrow a\left( t \right) = v'\left( t \right) =  - 0,06t + 2,2 = 0 \Leftrightarrow t \approx 37\).

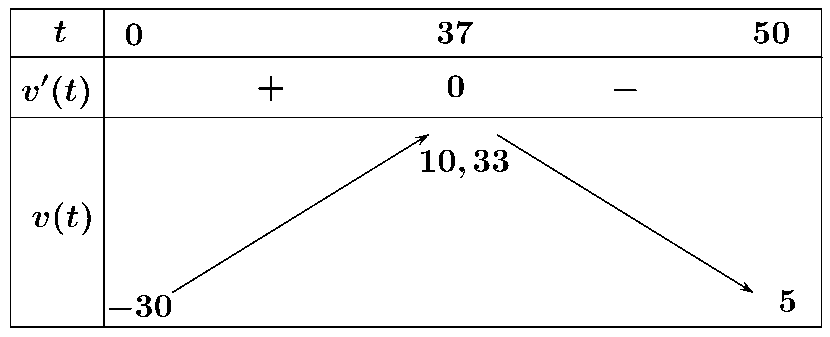
Vận tốc của con tàu lớn nhất mà con tàu đạt được là \(10,33\,\,\left( {{\rm{km/s}}} \right)\).

d) Sai. \(h\left( t \right) =  - 0,01{t^3} + 1,1{t^2} - 30t + 250 \Rightarrow v\left( t \right) = h'\left( t \right) =  - 0,03{t^2} + 2,2t - 30\)

\( \Rightarrow a\left( t \right) = v'\left( t \right) =  - 0,06t + 2,2 = 0 \Leftrightarrow t \approx 37\).

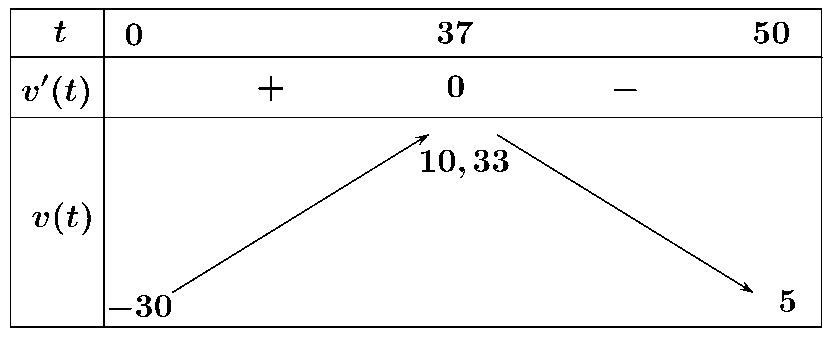
Khi đó: \({v_{{\rm{max}}}} = 10,33 \Leftrightarrow t \approx 37;\,\,\,\,h\left( {37} \right) = 139,37\)km.