Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho tam giác \(ABC\) biết \(AB = 8,AC = 9,BC = 11\). Gọi \(M\) là trung điểm \(BC\) và \(N\) là điểm trên đoạn \(AC\) sao cho \(AN = x\,(0 < x < 9)\). Hệ thức nào sau đây đúng?
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho tam giác \(ABC\) biết \(AB = 8,AC = 9,BC = 11\). Gọi \(M\) là trung điểm \(BC\) và \(N\) là điểm trên đoạn \(AC\) sao cho \(AN = x\,(0 < x < 9)\). Hệ thức nào sau đây đúng?A. \(\overrightarrow {MN} = \left( {\frac{1}{2} - \frac{x}{9}} \right)\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} \)
B. \(\overrightarrow {MN} = \left( {\frac{x}{9} - \frac{1}{2}} \right)\overrightarrow {CA} + \frac{1}{2}\overrightarrow {BA} \)
C. \(\overrightarrow {MN} = \left( {\frac{x}{9} + \frac{1}{2}} \right)\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \)
D. \(\overrightarrow {MN} = \left( {\frac{x}{9} - \frac{1}{2}} \right)\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \)
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương IV (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn D
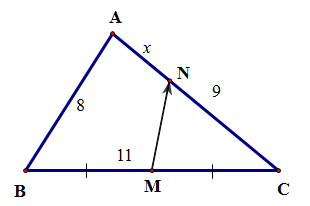
Ta có: \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \frac{x}{9}\overrightarrow {AC} - \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} ) = \left( {\frac{x}{9} - \frac{1}{2}} \right)\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(\overrightarrow {NM} = \frac{1}{3}\overrightarrow {AB} - \overrightarrow {AD} ,\overrightarrow {NP} = \frac{2}{3}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AD} \)
Suy ra \(\overrightarrow {NM} \cdot \overrightarrow {NP} = \frac{2}{9} \cdot 9 + \frac{1}{2} \cdot 9 = \frac{{13}}{2}\)
Mặt khác \(|\overrightarrow {NM} | = \sqrt {10} ,|\overrightarrow {NP} | = \frac{5}{2} \Rightarrow \cos \widehat {MNP} = \frac{{13}}{{5\sqrt {10} }}.\)
Lời giải
a) Do tứ giác \(BHC{A^\prime }\) có \(BH//{A^\prime }C( \bot AC)\) và \(CH//B{A^\prime }( \bot AB)\) nên \(BHC{A^\prime }\) là hình bình hành \( \Rightarrow \overrightarrow {BH} = \overrightarrow {{A^\prime }C} \)
b) Lại có \(M\) là trung điểm của đường chéo \(BC\) nên \(M\) là trung điểm của \(H{A^\prime }\) hay \(H,M\), \({A^\prime }\) thẳng hàng.
Do \(OM\) là đường trung bình của nên \(AH = 2OM\), mà \(\overrightarrow {AH} \) và \(\overrightarrow {OM} \) cùng hướng
\( \Rightarrow \overrightarrow {AH} = 2\overrightarrow {OM} {\rm{. }}\)
c) \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HA} \overrightarrow { + HA} \) (Tứ giác \(AHC{A^\prime }\) là hình bình hành \(\overrightarrow {H{A^\prime }} = \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \)
d) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} + \overrightarrow {HA} + \overrightarrow {OH} + \overrightarrow {HB} + \overrightarrow {OH} + \overrightarrow {HC} = 3\overrightarrow {OH} + \overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} \)
\( = 3\overrightarrow {OH} + 2\overrightarrow {HO} = \overrightarrow {OH} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {BC} \)
B. \(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {CA} \)
C. \(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {AB} \)
D. \(\overrightarrow {GM} = \frac{1}{3}\overrightarrow {CB} \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Miền (1)
B. Miền (2)
C. Miền (3)
D. Ở ngoài \(\Delta ABC\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo