Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí \(A\) đến trường. Trường của anh An ở vị trí \(B\) và trường của em Bình ở vị trí \(C\) theo hai hướng vuông góc với nhau (như hình vẽ). Anh An đi với tốc độ \(4\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 15 phút. Em Bình đi với tốc độ \(3\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 12 phút. Tính khoảng cách \(BC\) giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).
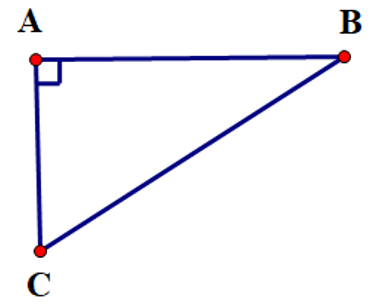
Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí \(A\) đến trường. Trường của anh An ở vị trí \(B\) và trường của em Bình ở vị trí \(C\) theo hai hướng vuông góc với nhau (như hình vẽ). Anh An đi với tốc độ \(4\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 15 phút. Em Bình đi với tốc độ \(3\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 12 phút. Tính khoảng cách \(BC\) giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).

Câu hỏi trong đề: Đề kiểm tra Toán 9 Chân trời sáng tạo Chương 3 có đáp án !!
Quảng cáo
Trả lời:
Quãng đường anh An đi từ nhà tới trường là: \(4 \cdot \frac{{15}}{{60}} = 1\,\,\left( {{\rm{km}}} \right)\).
Quãng đường em Bình từ nhà đến trường là \(3 \cdot \frac{{12}}{{60}} = 0,6\,\,\left( {{\rm{km}}} \right)\).
Áp dụng định lí Pythagore vào tam giác \(ABC\) vuông tại \(A\), ta có:
\(B{C^2} = A{B^2} + A{C^2} = {1^2} + {\left( {0,6} \right)^2} = 1,36\) hay \(BC = \sqrt {1,36} \approx 1,17\,\,\left( {{\rm{km}}} \right)\).
Vậy khoảng cách \(BC\) giữa hai trường khoảng \(1,17\,\,{\rm{km}}\).
Đáp án: 1,17.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Thay \(x = 180\) vào công thức \(h = 0,4\sqrt[3]{x}\), ta được:
\(h = 0,4 \cdot \sqrt[3]{{180}} \approx 2,26\;\,({\rm{m)}}{\rm{.}}\)
Vậy chiều cao của hươu cao cổ là \(2,26\;\,{\rm{m}}\).
Đáp án: 2,26.
Câu 2
Lời giải
Chọn C
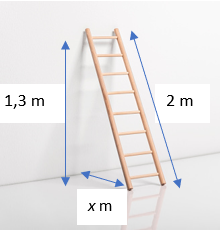
Áp dụng định lý Pythagore, ta có: \[{x^2} + {1,3^2} = {2^2}\].
Suy ra \[{x^2} = {2^2} - {1,3^2} = 2,31\].
Do đó, \[x = \sqrt {2,31} \approx 1,5\,\,({\rm{m)}}{\rm{.}}\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.