Cho hai hàm số \(y = 2{x^2}\) và \(y = - 2x + 4\).
a) Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ hai giao điểm \(A\) và \(B\) của hai đồ thị đó. Tính khoảng cách từ điểm \(M\left( { - 2;0} \right)\) đến đường thẳng \(AB.\)
Cho hai hàm số \(y = 2{x^2}\) và \(y = - 2x + 4\).
a) Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ hai giao điểm \(A\) và \(B\) của hai đồ thị đó. Tính khoảng cách từ điểm \(M\left( { - 2;0} \right)\) đến đường thẳng \(AB.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) • Vẽ đồ thị hàm số \(y = 2{x^2}\):
Hàm số \(y = 2{x^2}\) có hệ số \(a = 2 > 0\) nên hàm số đồng biến khi \(x > 0\), nghịch biến khi \(x < 0\) và đồ thị hàm số là parabol có bề lõm quay lên trên, nhận trục \(Oy\) làm trục đối xứng.
Bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = 2{x^2}\) |
8 |
2 |
0 |
2 |
8 |
Vậy đồ thị hàm số \(y = 2{x^2}\) là parabol đi qua các điểm \(\left( { - 2;8} \right),\left( { - 1;2} \right),\left( {0;0} \right),\left( {1;2} \right),\left( {2;8} \right)\).
• Vẽ đồ thị hàm số \(y = - 2x + 4\):
Cho \(x = 0\) thì \(y = 4\), ta được điểm \(\left( {0;4} \right)\).
Cho \(y = 0\) thì \(x = 2\), ta được điểm \(\left( {2;0} \right)\).
Đồ thị hàm số \(y = - 2x + 4\) là đường thẳng đi qua 2 điểm trên.
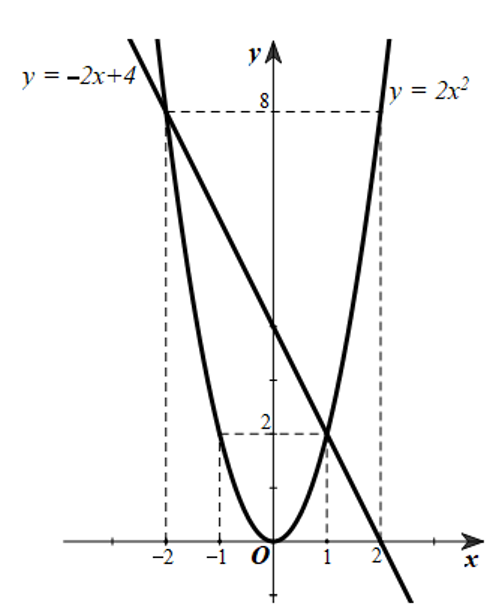
Ta vẽ các đồ thị hàm số \(y = 2{x^2}\) và \(y = - 2x + 4\) trên cùng một mặt phẳng tọa độ như sau:
b) Xét phương trình hoành độ giao điểm của đường thẳng \(y = - 2x + 4\)và parabol \(y = 2{x^2}\):
\( \Leftrightarrow {x^2} + x - 2 = 0\)
\( \Leftrightarrow {x^2} - x + 2x - 2 = 0\)
\( \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
Với \(x = 1 \Rightarrow y = 2\)
Với \(x = - 2 \Rightarrow y = 8\)
Vậy giao điểm của hai đồ thị hàm số đã cho là \(A\left( {1;2} \right);B\left( { - 2;8} \right)\).
* Tính khoảng cách từ \(M\left( { - 2;0} \right)\) đến đường thẳng \[AB\].
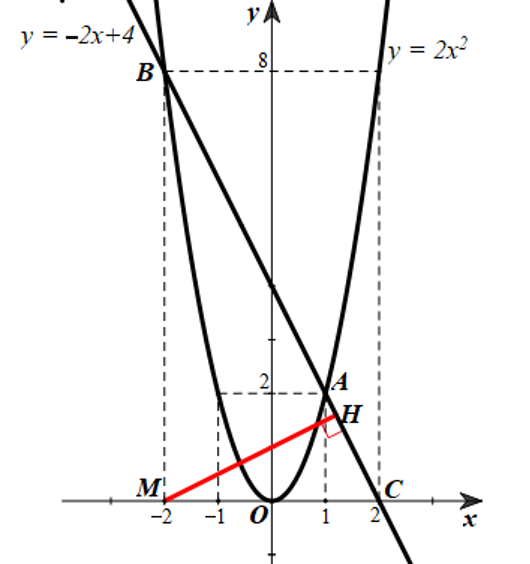
Kẻ \(MH \bot AB\left( {M \in AB} \right).\)
Do đó khoảng cách từ \(M\left( { - 2;0} \right)\) xuống đường thẳng \[AB\] chính là độ dài đoạn thẳng \(MH.\)
Gọi \(C\) là giao điểm của \(AB\) và \(Ox\) \( \Rightarrow C\left( {2;0} \right)\).
Dễ thấy \(\Delta MAC\) vuông tại \(M\), \(MA = 8,MC = 4\)
Áp dụng hệ thức lượng cho tam giác vuông \(\Delta MAC\), ta có:
\(\frac{1}{{M{H^2}}} = \frac{1}{{M{A^2}}} + \frac{1}{{M{C^2}}} = \frac{1}{{{8^2}}} + \frac{1}{{{4^2}}} = \frac{5}{{64}}\)
\( \Leftrightarrow MH = \frac{{8\sqrt 5 }}{5}\) (đơn vị dài)
Vậy khoảng cách cần tìm là \(MH = \frac{{8\sqrt 5 }}{5}\).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
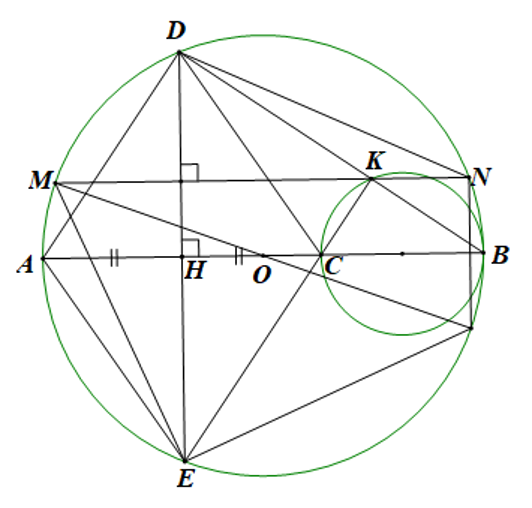
Ta có: \(\widehat {DHB} = 90^\circ \) (\(DE \bot AB\) tại \(H\)) \( \Rightarrow \widehat {DHC} = 90^\circ \)
\(\widehat {CKB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn đường kính BC) \( \Rightarrow \widehat {CKD} = 90^\circ \)
Xét tứ giác \(DHCK\)có \(\widehat {DHC} + \widehat {CKD} = 180^\circ \), mà hai góc ở vị trí đối diện nên tứ giác \(DHCK\)nội tiếp (tứ giác có tổng hai góc đối bằng \(180^\circ \)) (đpcm)
Có \(DE \bot AB \Rightarrow HD = HE\)(đường kính dây cung)
Lại có: \(HA = HC\) nên tứ giác \(DAEC\) là hình bình hành
\( \Rightarrow CE\,{\rm{//}}\,DA\) (điều phải chứng minh).
Lại có \(\widehat {CKB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn đường kính BC) \( \Rightarrow CK \bot KB(1)\)
Mà \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn đường kính AB) \( \Rightarrow AD \bot DB(2)\)
Từ (1) và (2) suy ra \(CK\,{\rm{//}}\,AD\) (từ vuông góc đến song song)
Mà \(CE\,{\rm{//}}\,AD(cmt)\) nên theo tiên đề Euclid suy ra ba điểm \(E,C,K\) thẳng hàng.
Kẻ đường kính \(MP\) của đường tròn \(\left( O \right)\).
Nối \(N\)với \(P\) cắt \[AB\] tại \(I\). Nối \(E\) với \(P\), \(E\) với \(B\).
Có \(\widehat {MNP} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow MN \bot NP\)
Mà \(MN \bot DE\) nên \(NP\,{\rm{//}}\,DE \Rightarrow DNPE\) là hình thang
Lại có \(DE \bot AB,NP//DE \Rightarrow NP \bot AB\)
\( \Rightarrow I\) là trung điểm của \[NP\] (tính chất đường kính dây cung)
\( \Rightarrow B\) là điểm chính giữa cung \(NP.\)
Dễ thấy tam giác \(BDE\) cân tại \(B\) (đường cao \(BH\) cũng là đường trung tuyến)
\( \Rightarrow DN = EP\) (hai dây bằng nhau căng hai cung bằng nhau)
Do đó: \(E{M^2} + D{N^2} = E{M^2} + E{P^2} = M{P^2}\) (Do tam giác \[MEP\] vuông tại \(E\))
Mà \(MP = AB\) (cùng là đường trình của đường tròn \(\left( O \right)\)).
Vậy \(E{M^2} + E{P^2} = A{B^2}\) (điều phải chứng minh).
Lời giải
Với \(x \ge - 1\), ta có:
\(B = \sqrt {9x + 9} + \sqrt {4x + 4} + \sqrt {x + 1} \)
\( = \sqrt {9\left( {x + 1} \right)} + \sqrt {4\left( {x + 1} \right)} + \sqrt {x + 1} \)
\( = 3\sqrt {x + 1} + 2\sqrt {x + 1} + \sqrt {x + 1} \)
\( = 6\sqrt {x + 1} \).
Ta có: \(B = 18 \Leftrightarrow 6\sqrt {x + 1} = 18 \Leftrightarrow \sqrt {x + 1} = 3 \Leftrightarrow x + 1 = 9 \Leftrightarrow x = 8(tm)\)
Vậy \(x = 8\) thì \(B = 18\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo