Chị Lan đun sôi nước bằng ấm điện. Biết rằng mối liên hệ giữa công suất hao phí \(P\left( W \right)\) của ấm điện và thời gian đun \(t\) (giây) được mô hình hóa bởi một hàm số bậc nhất có dạng \(P = at + b\) và có đồ thị như hình bên.
a) Hãy xác định các hệ số \(a\) và \(b\).
b) Nếu đun nước với công suất hao phí là \(105\left( W \right)\) thì thời gian đun là bao lâu?
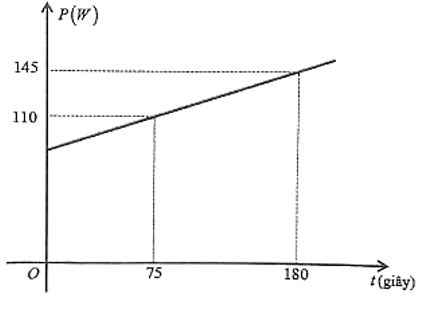
Chị Lan đun sôi nước bằng ấm điện. Biết rằng mối liên hệ giữa công suất hao phí \(P\left( W \right)\) của ấm điện và thời gian đun \(t\) (giây) được mô hình hóa bởi một hàm số bậc nhất có dạng \(P = at + b\) và có đồ thị như hình bên.
a) Hãy xác định các hệ số \(a\) và \(b\).
b) Nếu đun nước với công suất hao phí là \(105\left( W \right)\) thì thời gian đun là bao lâu?

Quảng cáo
Trả lời:
a) Quan sát đồ thị ta thấy:
Tại thời điểm \(t = 75\) (giây) thì công suất hao phí là \(110W\) nên đồ thị hàm số \(P = at + b\) đi qua điểm \(\left( {75;\,110} \right)\). Ta có phương trình: \(110 = 75a + b\). (1)
Tại thời điểm \(t = 180\) (giây) thì công suất hao phí là \(145\,W\) nên đồ thị hàm số \(P = at + b\) đi qua điểm \(\left( {180;\,145} \right)\). Ta có phương trình: \(145 = 180a + b\). (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}110 = 75a + b\\145 = 180a + b\end{array} \right.\) (0,25 điểm)
\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{3}\\b = 85\end{array} \right.\). (0,25 điểm)
Vậy các hệ số cần tìm là \(a = \frac{1}{3},\,b = 85\).
b) Từ câu a) ta có: \(P = \frac{1}{3}t + 85\). Gọi \({t_0}\) (giây) là thời gian đun nước với công suất hao phí là \(P\left( {{t_0}} \right) = 105\,W\), ta có phương trình
\(\frac{1}{3}{t_0} + 85 = 105\) (0,25 điểm)
\( \Leftrightarrow {t_0} = 60\). (0,25 điểm)
Vậy thời gian để đun nước với công suất hao phí \(105\left( W \right)\) là 60 giây.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
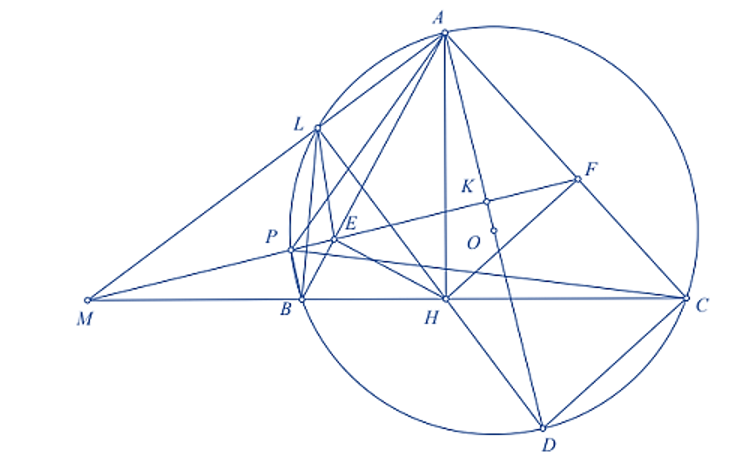
a) Ta có: \(HE \bot AB,\,HF \bot AC\) nên \(\widehat {AEH} = \widehat {AFH} = 90^\circ \). Tứ giác \(AEHF\) có \(\widehat {AEH},\,\widehat {AFH}\) là hai góc đối và \(\widehat {AEH} + \,\widehat {AFH} = 90^\circ + 90^\circ = 180^\circ \) nên tứ giác \(AEHF\) nội tiếp. (0,5 điểm)
Do \(AD\) là đường kính của đường tròn \(\left( O \right)\) nên \(\widehat {ALD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Tứ giác \(ALHF\) có \(\widehat {ALH},\,\widehat {AFH}\) là hai góc đối và \(\widehat {ALH} + \,\widehat {AFH} = 90^\circ + 90^\circ = 180^\circ \) nên tứ giác \(ALHF\) nội tiếp. (0,5 điểm)
b) Ta có: \(AH \bot BC\) và \(HE \bot AB\) nên \(\widehat {EBH} = 90^\circ - \widehat {BHE} = \widehat {AHE}\).
Mà \(\widehat {AHE} = \widehat {AFE}\) (do tứ giác \(AEHF\) nội tiếp).
Suy ra \(\widehat {AFE} = \widehat {EBC}\) (1).
Tứ giác \(BEFC\) có góc ngoài tại đỉnh \(F\) bằng góc trong tại đỉnh \(B\) nên tứ giác \(BEFC\) nội tiếp. (0,5 điểm)
Trong đường tròn \(\left( O \right)\), ta có \(\widehat {ABC} = \widehat {ADC}\) (hai góc nội tiếp chắn cung \(AC\)) (2).
Từ (1) và (2) suy ra \(\widehat {AFE} = \widehat {ADC}\) hay \[\widehat {AFK} = \widehat {KDC}\].
Tứ giác \(CDKF\) có góc ngoài tại đỉnh \(F\) bằng góc trong tại đỉnh \(D\) nên tứ giác \(CDKF\) nội tiếp.
Suy ra \(\widehat {DKF} + \widehat {CKF} = 180^\circ \).
Mặt khác \(\widehat {ACD} = 90^\circ \) (do \(AD\) là đường kính của \(\left( O \right)\)).
Từ đó suy ra \(\widehat {DKF} = 90^\circ \). Suy ra \(AD \bot EF\) tại \(K\). (0,5 điểm)
c) Tứ giác \(APBC\) nội tiếp đường tròn \(\left( O \right)\) nên \(\widehat {APC} = \widehat {ABC}\). (3)
Từ (1) và (3) suy ra \(\widehat {APC} = \widehat {AFE}\).
Do đó, hai tam giác \(APF\) và \(ACP\) đồng dạng (g.g).
Suy ra \(\frac{{AP}}{{AC}} = \frac{{AF}}{{AP}}\).
Nên \(A{P^2} = AC.AF\). (0,25 điểm)
Lại có \(A{H^2} = AC.AF\) (áp dụng hệ thức lượng trong tam giác \(ACH\) vuông tại \(H\) có đường cao \(HF\)).
Do đó, \(A{P^2} = A{H^2}\). Suy ra \(AP = AH\). (0,25 điểm)
Vì các tứ giác \(AEHF,\,ALHF\) nội tiếp nên năm điểm \(A,\,E,\,F,\,H,\,L\) cùng thuộc một đường tròn.
Suy ra tứ giác \(ALEF\) nội tiếp.
Từ đó suy ra \(\widehat {MEL} = \widehat {LAF}\) (cùng bù với \(\widehat {LEF}\)).
Lập luận tương tự với tứ giác nội tiếp \(ALBC\), ta có \(\widehat {MBL} = \widehat {LAC}\).
Từ hai điều trên, suy ra \(\widehat {MBL} = \widehat {MEL}\).
Tứ giác \(MBEL\) có hai đỉnh kề nhau là \(B,\,E\) cùng nhìn cạnh \(ML\) dưới hai góc bằng nhau nên tứ giác \(MBEL\) nội tiếp. (0,25 điểm)
Suy ra \(\widehat {MLE} = \widehat {EBC}\) (cùng bù với \(\widehat {MBE}\)). (4)
Từ (1) và (4) suy ra \(\widehat {MLE} = \widehat {AFE}\).
Lại có \(\widehat {AFE} + \widehat {ALE} = 180^\circ \) (do tứ giác \(ALEF\) nội tiếp).
Do đó, \(\widehat {MLE} + \widehat {ALE} = 180^\circ \).
Vậy ba điểm \(A,\,L,\,M\) thẳng hàng. (0,25 điểm)
Lời giải
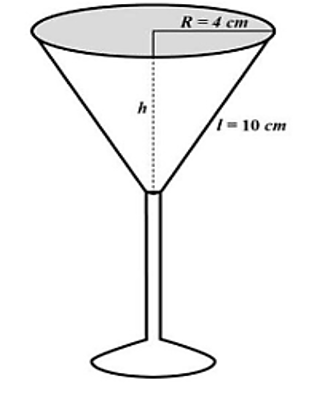
a) Theo định lí Pythagore, chiều cao của hình nón là
\(h = \sqrt {{l^2} - {R^2}} = \sqrt {{{10}^2} - {4^2}} = 2\sqrt {21} \) (cm). (0,25 điểm)
Thể tích phần chứa nước của ly là
\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.4^2}.2\sqrt {21} \approx 154\) (cm3). (0,25 điểm)
b) Đổi 1,2 lít = 1200 cm3.
Số ly nước Nam cần chuẩn bị là: 14 . 3 = 42 (ly).
Lượng nước trái cây Nam cần chuẩn bị là: (154 . 90%) . 42 = 5821,2 (cm3). (0,25 điểm)
Ta có: \(\frac{{5821,2}}{{1200}} = 4,851 \approx 5\).
Vậy Nam cần chuẩn bị 5 hộp nước trái cây.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.