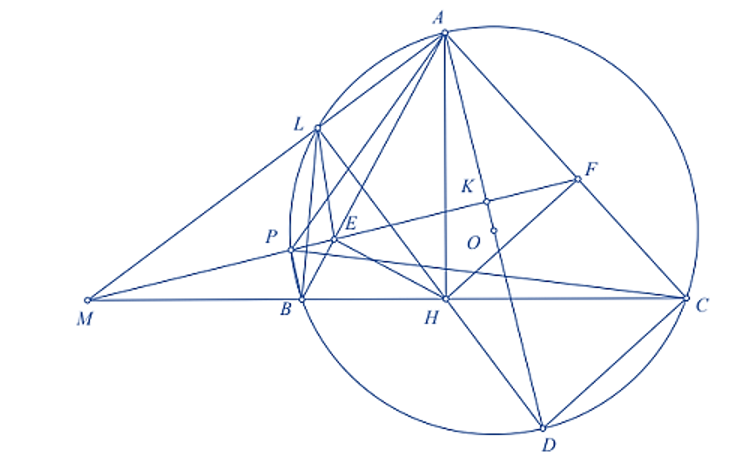
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) có đường cao \(AH\) và nội tiếp đường tròn \(\left( O \right)\). Gọi \(E,\,F\) lần lượt là hình chiếu của \(H\) lên các cạnh \(AB,\,AC\). Đường kính \(AD\) của \(\left( O \right)\) cắt \(EF\) tại \(K\) và \(DH\) cắt\(\left( O \right)\) tại \(L\) (\(L\) khác \(D\)).
a) Chứng minh các tứ giác \(AEHF\) và \(ALHF\) nội tiếp.
b) Chứng minh tứ giác \(BEFC\) nội tiếp và \(AD\) vuông góc với \(EF\) tại \(K\).
c) Tia \(FE\) cắt \(\left( O \right)\) tại \(P\) và cắt \(BC\) tại \(M\). Chứng minh \[AP = AH\] và ba điểm \(A,\,L,\,M\) thẳng hàng.
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) có đường cao \(AH\) và nội tiếp đường tròn \(\left( O \right)\). Gọi \(E,\,F\) lần lượt là hình chiếu của \(H\) lên các cạnh \(AB,\,AC\). Đường kính \(AD\) của \(\left( O \right)\) cắt \(EF\) tại \(K\) và \(DH\) cắt\(\left( O \right)\) tại \(L\) (\(L\) khác \(D\)).
a) Chứng minh các tứ giác \(AEHF\) và \(ALHF\) nội tiếp.
b) Chứng minh tứ giác \(BEFC\) nội tiếp và \(AD\) vuông góc với \(EF\) tại \(K\).
c) Tia \(FE\) cắt \(\left( O \right)\) tại \(P\) và cắt \(BC\) tại \(M\). Chứng minh \[AP = AH\] và ba điểm \(A,\,L,\,M\) thẳng hàng.
Quảng cáo
Trả lời:
a) Ta có: \(HE \bot AB,\,HF \bot AC\) nên \(\widehat {AEH} = \widehat {AFH} = 90^\circ \). Tứ giác \(AEHF\) có \(\widehat {AEH},\,\widehat {AFH}\) là hai góc đối và \(\widehat {AEH} + \,\widehat {AFH} = 90^\circ + 90^\circ = 180^\circ \) nên tứ giác \(AEHF\) nội tiếp. (0,5 điểm)
Do \(AD\) là đường kính của đường tròn \(\left( O \right)\) nên \(\widehat {ALD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Tứ giác \(ALHF\) có \(\widehat {ALH},\,\widehat {AFH}\) là hai góc đối và \(\widehat {ALH} + \,\widehat {AFH} = 90^\circ + 90^\circ = 180^\circ \) nên tứ giác \(ALHF\) nội tiếp. (0,5 điểm)
b) Ta có: \(AH \bot BC\) và \(HE \bot AB\) nên \(\widehat {EBH} = 90^\circ - \widehat {BHE} = \widehat {AHE}\).
Mà \(\widehat {AHE} = \widehat {AFE}\) (do tứ giác \(AEHF\) nội tiếp).
Suy ra \(\widehat {AFE} = \widehat {EBC}\) (1).
Tứ giác \(BEFC\) có góc ngoài tại đỉnh \(F\) bằng góc trong tại đỉnh \(B\) nên tứ giác \(BEFC\) nội tiếp. (0,5 điểm)
Trong đường tròn \(\left( O \right)\), ta có \(\widehat {ABC} = \widehat {ADC}\) (hai góc nội tiếp chắn cung \(AC\)) (2).
Từ (1) và (2) suy ra \(\widehat {AFE} = \widehat {ADC}\) hay \[\widehat {AFK} = \widehat {KDC}\].
Tứ giác \(CDKF\) có góc ngoài tại đỉnh \(F\) bằng góc trong tại đỉnh \(D\) nên tứ giác \(CDKF\) nội tiếp.
Suy ra \(\widehat {DKF} + \widehat {CKF} = 180^\circ \).
Mặt khác \(\widehat {ACD} = 90^\circ \) (do \(AD\) là đường kính của \(\left( O \right)\)).
Từ đó suy ra \(\widehat {DKF} = 90^\circ \). Suy ra \(AD \bot EF\) tại \(K\). (0,5 điểm)
c) Tứ giác \(APBC\) nội tiếp đường tròn \(\left( O \right)\) nên \(\widehat {APC} = \widehat {ABC}\). (3)
Từ (1) và (3) suy ra \(\widehat {APC} = \widehat {AFE}\).
Do đó, hai tam giác \(APF\) và \(ACP\) đồng dạng (g.g).
Suy ra \(\frac{{AP}}{{AC}} = \frac{{AF}}{{AP}}\).
Nên \(A{P^2} = AC.AF\). (0,25 điểm)
Lại có \(A{H^2} = AC.AF\) (áp dụng hệ thức lượng trong tam giác \(ACH\) vuông tại \(H\) có đường cao \(HF\)).
Do đó, \(A{P^2} = A{H^2}\). Suy ra \(AP = AH\). (0,25 điểm)
Vì các tứ giác \(AEHF,\,ALHF\) nội tiếp nên năm điểm \(A,\,E,\,F,\,H,\,L\) cùng thuộc một đường tròn.
Suy ra tứ giác \(ALEF\) nội tiếp.
Từ đó suy ra \(\widehat {MEL} = \widehat {LAF}\) (cùng bù với \(\widehat {LEF}\)).
Lập luận tương tự với tứ giác nội tiếp \(ALBC\), ta có \(\widehat {MBL} = \widehat {LAC}\).
Từ hai điều trên, suy ra \(\widehat {MBL} = \widehat {MEL}\).
Tứ giác \(MBEL\) có hai đỉnh kề nhau là \(B,\,E\) cùng nhìn cạnh \(ML\) dưới hai góc bằng nhau nên tứ giác \(MBEL\) nội tiếp. (0,25 điểm)
Suy ra \(\widehat {MLE} = \widehat {EBC}\) (cùng bù với \(\widehat {MBE}\)). (4)
Từ (1) và (4) suy ra \(\widehat {MLE} = \widehat {AFE}\).
Lại có \(\widehat {AFE} + \widehat {ALE} = 180^\circ \) (do tứ giác \(ALEF\) nội tiếp).
Do đó, \(\widehat {MLE} + \widehat {ALE} = 180^\circ \).
Vậy ba điểm \(A,\,L,\,M\) thẳng hàng. (0,25 điểm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
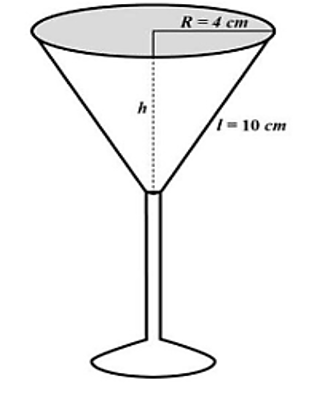
a) Theo định lí Pythagore, chiều cao của hình nón là
\(h = \sqrt {{l^2} - {R^2}} = \sqrt {{{10}^2} - {4^2}} = 2\sqrt {21} \) (cm). (0,25 điểm)
Thể tích phần chứa nước của ly là
\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.4^2}.2\sqrt {21} \approx 154\) (cm3). (0,25 điểm)
b) Đổi 1,2 lít = 1200 cm3.
Số ly nước Nam cần chuẩn bị là: 14 . 3 = 42 (ly).
Lượng nước trái cây Nam cần chuẩn bị là: (154 . 90%) . 42 = 5821,2 (cm3). (0,25 điểm)
Ta có: \(\frac{{5821,2}}{{1200}} = 4,851 \approx 5\).
Vậy Nam cần chuẩn bị 5 hộp nước trái cây.Lời giải
Gọi lượng sữa ban đầu của thùng thứ nhất chứa là \(x\) (lít) và lượng sữa thùng thứ hai chứa là \(y\) (lít), ta có \(0 < x \le 10,\,0 < y \le 8\) và tổng lượng sữa \(x + y > 10\). (0,25 điểm)
- Vì sau khi đổ sữa từ thùng thứ nhất sang thùng thứ hai cho đầy thì thùng thứ hai có 8 lít sữa, còn thùng thứ nhất có \(x + y - 8\) lít sữa.
Lúc này lượng sữa còn lại ở thùng thứ nhất bằng \(\frac{1}{2}\) lượng sữa so với ban đầu nên ta có phương trình:
\(x + y - 8 = \frac{1}{2}x \Leftrightarrow \frac{1}{2}x + y = 8\). (1)
- Vì sau khi đổ sữa từ thùng thứ hai sang thùng thứ nhất cho đầy thì thùng thứ nhất có 10 lít sữa, còn thùng thứ hai có \(x + y - 10\) lít sữa.
Lúc này thùng thứ hai có lượng sữa bằng \(\frac{1}{5}\) lượng sữa so với thời điểm ban đầu nên ta có phương trình:
\(x + y - 10 = \frac{1}{5}y \Leftrightarrow x + \frac{4}{5}y = 10\). (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{2}x + y = 8\\x + \frac{4}{5}y = 10\end{array} \right.\) (0,5 điểm)
\( \Leftrightarrow \left\{ \begin{array}{l}x + 2y = 16\\x + \frac{4}{5}y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{6}{5}y = 6\\x = 10 - \frac{4}{5}y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5\\x = 6\end{array} \right.\) (thỏa mãn). (0,25 điểm)
Vậy thời điểm ban đầu thùng thứ nhất chứa 6 lít sữa, thùng thứ hai chứa 5 lít sữa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.