Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm \[A\]) đến trường (điểm \[B\]) phải leo lên và xuống một con dốc (như hình vẽ bên dưới). Cho biết đoạn thẳng \[AB\] dài 762 m, góc \[A\] = 6°, góc \[B\] = 4°.

a) Tính chiều cao \(h\) của con dốc.

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ trung bình xuống dốc là 19 km/h.

a) Ta có: \[\widehat {ADB} = 90^\circ \] (góc nội tiếp chẵn nửa đường tròn) \[ \Rightarrow \widehat {ADC} = 90^\circ \]

\[ \Rightarrow \widehat {ADC} = \widehat {AHC}\]\[ \Rightarrow ACDH\] nội tiếp.

\[ \Rightarrow \widehat {CHD} = \widehat {CAD}\]

Mà \[\widehat {CAD} = \widehat {ABC}\] nên \[\widehat {CHD} = \widehat {ABC}\].

b) Ta có: \[OH.OC = O{A^2} = O{B^2} \Rightarrow \frac{{OH}}{{OB}} = \frac{{OB}}{{OC}}\]

.

\[ \Rightarrow \widehat {OHB} = \widehat {OBC} \Rightarrow \widehat {OHB} = \widehat {CHD}\]

\[ \Rightarrow \widehat {BHM} = \widehat {DHM}\] hay \[HM\] là tia phân giác của góc \[BHD\].

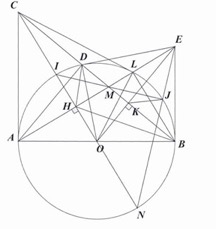
c) Tam giác \[DHB\] có \[HM\] là phân giác trong \[ \Rightarrow \frac{{MD}}{{MB}} = \frac{{HD}}{{HB}}\]

Tam giác \[DHB\] có \[HC\] là phân giác ngoài \[ \Rightarrow \frac{{CD}}{{CB}} = \frac{{HD}}{{HB}}\]

Vậy \[\frac{{MD}}{{MB}} = \frac{{CD}}{{CB}} \Rightarrow MD.BC = MB.CD\].

Cách 1. Từ trên suy ra \[MD.\left( {MB + MC} \right) = MB.\left( {MC - MD} \right)\]

\[ \Rightarrow 2MB.MD = MC\left( {MB - MD} \right)\]

\[ \Rightarrow 2MB.MD = 2MK.MC\]

\[ \Rightarrow MB.MD = MK.MC\]

Cách 2. Gọi \[L\] là giao điểm của \[AE\] với đường tròn \[\left( O \right)\].

5 điểm \[A,\,O,\,K,\,L,\,C\] cùng thuộc đường tròn.

\[ \Rightarrow MK.MC = MA.ML\]

Mà \[MA.ML = MB.MD\]\[ \Rightarrow MB.MD = MK.MC\].

d) Gọi \[N\] là giao điểm của \[CO\,\]với đường tròn \[\left( O \right)\].

\[ \Rightarrow \widehat {IJN} = 90^\circ \,\,\left( 1 \right)\]

Mặt khác: \[MI.MJ = MD.MB = MK.MC\]

\[ \Rightarrow \widehat {MCI} = \widehat {MJK} = \widehat {MEO}\]

\[ \Rightarrow MEJK\] nội tiếp.

\[ \Rightarrow \widehat {EJM} = 90^\circ \,\,\,\,\left( 2 \right)\]

Từ (1) và (2) \[ \Rightarrow E,\,\,J,\,\,N\] thẳng hàng.

Suy ra hai đường thẳng \[OC\] và \[EJ\] cắt nhau tại một điểm nằm trên \[\,\left( O \right)\].

a) Vẽ đồ thị hàm số \(y = \frac{1}{4}{x^2}\).

Tập xác định \[D = \mathbb{R}\].

Bảng giá trị

Đồ thị

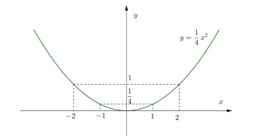
b) Đường thẳng \[\left( D \right)\]: \(y = \frac{3}{2}x + m\) đi qua điểm \[C\left( {6;\,7} \right)\]nên ta có:

\[7 = \frac{3}{2}.6 + m \Leftrightarrow m =  - 2\].

Vậy đường thẳng \[\left( D \right)\] có phương trình \[y = \frac{3}{2}x - 2\].

Phương trình hoành độ giao điểm của \[\left( D \right)\] và \[\left( P \right)\] là \[\frac{1}{4}{x^2} = \frac{3}{2}x - 2\]

\[ \Leftrightarrow \frac{1}{4}{x^2} - \frac{3}{2}x + 2 = 0 \Leftrightarrow {x^2} - 6x + 8 = 0\]

Ta có: \[\Delta ' = {\left( { - 3} \right)^2} - 1.8 = 1 > 0\]. Phương trình có hai nghiệm \[{x_1} = 3 + 1 = 4,\,{x_2} = 3 - 1 = 2\]

Khi đó, \[{y_1} = \frac{3}{2}{x_1} - 2 = \frac{3}{2}.4 - 2 = 4,\,{y_2} = \frac{3}{2}{x_2} - 2 = \frac{3}{2}.2 - 2 = 1\].

Vậy tọa độ các giao điểm của \[\left( D \right)\] và \[\left( P \right)\] là \[A\left( {4;\,\,4} \right),\,\,B\left( {2;\,\,1} \right)\].