Năm học 2017 – 2018, Trường THCS Tiến Thành có ba lớp 9 gồm 9A, 9B, 9C trong đó lớp 9A có 35 học sinh và lớp 9B có 40 học sinh. Tổng kết cuối năm học, lớp 9A có 15 học sinh đạt danh hiệu học sinh giỏi, lớp 9B có 12 học sinh đạt danh hiệu học sinh giỏi, lớp 9C có 20% học sinh đạt danh hiệu học sinh giỏi và toàn khối 9 có 30% học sinh đạt danh hiệu học sinh giỏi. Hỏi lớp 9C có bao nhiêu học sinh?
Năm học 2017 – 2018, Trường THCS Tiến Thành có ba lớp 9 gồm 9A, 9B, 9C trong đó lớp 9A có 35 học sinh và lớp 9B có 40 học sinh. Tổng kết cuối năm học, lớp 9A có 15 học sinh đạt danh hiệu học sinh giỏi, lớp 9B có 12 học sinh đạt danh hiệu học sinh giỏi, lớp 9C có 20% học sinh đạt danh hiệu học sinh giỏi và toàn khối 9 có 30% học sinh đạt danh hiệu học sinh giỏi. Hỏi lớp 9C có bao nhiêu học sinh?
Quảng cáo
Trả lời:
Gọi \[x\] là số học sinh lớp 9C (\[x \in \mathbb{N}\]).
Ta có:
Tổng số học sinh của 3 lớp là: \[x + 35 + 40 = x + 75\] (học sinh).
Tổng số học sinh giỏi của 3 lớp là: \[15 + 12 + x.20\% = 27 + \frac{1}{5}x\] (học sinh).
Vì toàn khối 9 có 30% học sinh đạt danh hiệu học sinh giỏi nên ta có phương trình:
\[27 + \frac{1}{5}x = \left( {x + 75} \right).30\% \]
\[ \Leftrightarrow 27 + \frac{1}{5}x = \left( {x + 75} \right).\frac{3}{{10}}\]
\[ \Leftrightarrow 270 + 2x = 3x + 225\]
\[ \Rightarrow x = 270 - 225 = 45\].
Vậy lớp 9C có 45 học sinh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \[BD = \sqrt {B{C^2} + C{D^2}} = \sqrt {{{230}^2} + {{230}^2}} = 230\sqrt 2 \] (m) (định lí Pytago trong tam giác vuông \[BCD\]).
Suy ra \[OD = \frac{{BD}}{2} = \frac{{230\sqrt 2 }}{2} = \frac{{230}}{{\sqrt 2 }}\] (m).
Khi đó \[S{O^2} = S{D^2} - O{D^2} = {214^2} - \frac{{{{230}^2}}}{2} = 19346\] (định lí Pytago trong tam giác vuông \[SOD\])
\[ \Rightarrow SO = \sqrt {19346} \approx 139,1\] (m).
Vậy \[h = SO \approx 139,1\] (m).
b) Tacó \[V = \frac{1}{3}S.h \approx \frac{1}{3}{.230^2}.139,1 \approx 2452796,667 \approx 2\,\,453\,\,000\] (m3).
Lời giải
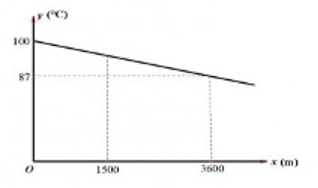
a) Từ đề bài ta có: \[100 = 0a + b \Rightarrow b = 100\]
\[87 = 3600a + b \Rightarrow a = \frac{{87 - b}}{{3600}} = \frac{{87 - 100}}{{3600}} = - \frac{{13}}{{3600}}\].
Vậy \[a = - \frac{{13}}{{3600}},\,\,b = 100\].
b) Ta có hàm số: \[y = - \frac{{13}}{{3600}}x + 100\].
Nhiệt độ sôi của Đà Lạt là: \[y = - \frac{{13}}{{3600}}.1500 + 100 \approx 94,583^\circ {\rm{C}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.