Cho tam giác nhọn \[ABC\] có \[BC = 8\] cm. Đường tròn tâm \[O\] đường kính \[BC\] cắt \[AB,\,\,AC\]lần lượt tại \[E\] và \[D\]. Hai đường thẳng \[BD\] và \[CE\] cắt nhau tại \[H\].
a) Chứng minh: \[AH\] vuông góc với \[BC\].
b) Gọi \[K\] là trung điểm của \[AH\]. Chứng minh tứ giác \[OEKD\] nội tiếp.
c) Cho góc \[\widehat {BAC} = 60^\circ \]. Tính độ dài đoạn \[DE\] và tỉ số diện tích của hai tam giác \[AED\] và \[ABC\].
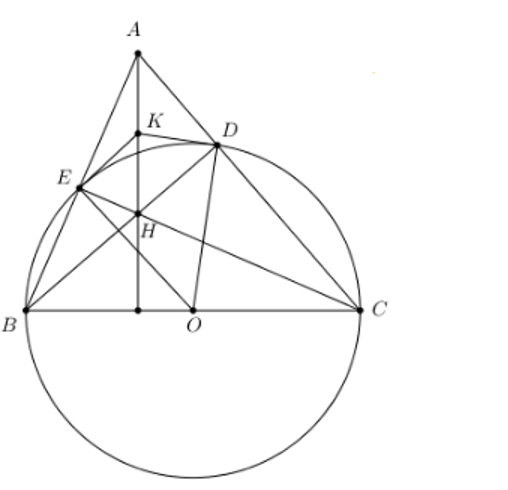
Cho tam giác nhọn \[ABC\] có \[BC = 8\] cm. Đường tròn tâm \[O\] đường kính \[BC\] cắt \[AB,\,\,AC\]lần lượt tại \[E\] và \[D\]. Hai đường thẳng \[BD\] và \[CE\] cắt nhau tại \[H\].
a) Chứng minh: \[AH\] vuông góc với \[BC\].
b) Gọi \[K\] là trung điểm của \[AH\]. Chứng minh tứ giác \[OEKD\] nội tiếp.
c) Cho góc \[\widehat {BAC} = 60^\circ \]. Tính độ dài đoạn \[DE\] và tỉ số diện tích của hai tam giác \[AED\] và \[ABC\].
Quảng cáo
Trả lời:
a) Ta có: \[\widehat {BEC} = \widehat {BDC} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn).
Suy ra \[CE \bot AB,\,\,BD \bot AC\].
Khi đó, tam giác \[ABC\] có 2 đường cao \[BD\] và \[CE\] cắt nhau tại \[H\] nên \[H\] là trực tâm của tam giác \[ABC\]. Nên \[AH\] là một đường cao của tam giác \[ABC\].
Suy ra \[AH\] vuông góc \[BC\].
b) Ta có: \[\widehat {AEH} + \widehat {ADH} = 90^\circ + 90^\circ = 180^\circ \].
Suy ra tứ giác \[ADHE\] là tứ giác nội tiếp đường tròn đường kính \[AH\].
Vì \[K\] là trung điểm của \[AH\] nên \[K\] là tâm của đường tròn đường kính \[AH\].
\[ \Rightarrow \widehat {EKD} = 2\widehat {EAD}\] (tính chất góc ở tâm)
Lại có: \[\widehat {EOD} = 2\widehat {EBD}\] (tính chất góc ở tâm)
Suy ra \[\widehat {EKD} + \widehat {EOD} = 2\left( {\widehat {EAD} + \widehat {EBD}} \right) = 2.90^\circ = 180^\circ \] (do tam giác \[ABD\] vuông tại \[D\])
Mà \[\widehat {EKD}\] và \[\widehat {EOD}\] là hai góc đối diện trong tứ giác \[OEKD\].
Vậy tứ giác \[OEKD\] nội tiếp.
c) +) Tam giác \[ABD\] vuông tại \[D\] và có \[\widehat {BAD} = \widehat {BAC} = 60^\circ \].
Suy ra \[\widehat {ABD} = 90^\circ - \widehat {BAD} = 90^\circ - 60^\circ = 30^\circ \].
Suy ra \[\widehat {EOD} = 2\widehat {EBD} = 2\widehat {ABD} = 2.30^\circ = 60^\circ \].
Lại có tam giác \[OED\] có \[OE = OD\] (cùng bằng bán kính) và \[\widehat {EOD} = 60^\circ \] nên \[OED\] là tam giác đều.
Suy ra \[DE = OE = \frac{{BC}}{2} = \frac{8}{2} = 4\] (cm).
+) Tứ giác \[BEDC\] nội tiếp đường tròn \[\left( O \right)\].
\[ \Rightarrow \widehat {ABC} + \widehat {EDC} = 180^\circ \]
Mà \[\widehat {EDC} + \widehat {ADE} = 180^\circ \] (kề bù)
Nên \[\widehat {ABC} = \widehat {ADE}\].
Xét \[\Delta ADE\] và \[\Delta ABC\] có
\[\widehat A:{\rm{chung}}\]
\[\widehat {ABC} = \widehat {ADE}\]
Do đó, (g – g).
Suy ra \[\frac{{{S_{ADE}}}}{{S{ & _{ABC}}}} = {\left( {\frac{{DE}}{{BC}}} \right)^2} = {\left( {\frac{4}{8}} \right)^2} = \frac{1}{4}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \[BD = \sqrt {B{C^2} + C{D^2}} = \sqrt {{{230}^2} + {{230}^2}} = 230\sqrt 2 \] (m) (định lí Pytago trong tam giác vuông \[BCD\]).
Suy ra \[OD = \frac{{BD}}{2} = \frac{{230\sqrt 2 }}{2} = \frac{{230}}{{\sqrt 2 }}\] (m).
Khi đó \[S{O^2} = S{D^2} - O{D^2} = {214^2} - \frac{{{{230}^2}}}{2} = 19346\] (định lí Pytago trong tam giác vuông \[SOD\])
\[ \Rightarrow SO = \sqrt {19346} \approx 139,1\] (m).
Vậy \[h = SO \approx 139,1\] (m).
b) Tacó \[V = \frac{1}{3}S.h \approx \frac{1}{3}{.230^2}.139,1 \approx 2452796,667 \approx 2\,\,453\,\,000\] (m3).
Lời giải
Gọi \[x\] là số học sinh lớp 9C (\[x \in \mathbb{N}\]).
Ta có:
Tổng số học sinh của 3 lớp là: \[x + 35 + 40 = x + 75\] (học sinh).
Tổng số học sinh giỏi của 3 lớp là: \[15 + 12 + x.20\% = 27 + \frac{1}{5}x\] (học sinh).
Vì toàn khối 9 có 30% học sinh đạt danh hiệu học sinh giỏi nên ta có phương trình:
\[27 + \frac{1}{5}x = \left( {x + 75} \right).30\% \]
\[ \Leftrightarrow 27 + \frac{1}{5}x = \left( {x + 75} \right).\frac{3}{{10}}\]
\[ \Leftrightarrow 270 + 2x = 3x + 225\]
\[ \Rightarrow x = 270 - 225 = 45\].
Vậy lớp 9C có 45 học sinh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.