Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm (atmosphere). Bên dưới mặt nước, áp suất nước tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất \(y\) (atm) và độ sâu \(x\) (m) dưới mặt nước là một hàm số bậc nhất có dạng \(y = ax + b\).
a) Xác định các hệ số \(a\)và \(b\).
b) Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất 2,85 atm?
Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm (atmosphere). Bên dưới mặt nước, áp suất nước tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất \(y\) (atm) và độ sâu \(x\) (m) dưới mặt nước là một hàm số bậc nhất có dạng \(y = ax + b\).
a) Xác định các hệ số \(a\)và \(b\).
b) Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất 2,85 atm?
Quảng cáo
Trả lời:
a) Nếu \(x = 0 \Rightarrow y = 1 \Rightarrow b = 1\)
Nếu \(x\)tăng 10 thì \(y\) tăng 1, suy ra \(x = 10 \Rightarrow y = 2 \Rightarrow a = \frac{1}{{10}}\)
Vậy \(y = \frac{1}{{10}}x + 1\).
b) Người thợ lặn chịu được áp suất 2,85 atm nên ta có:
\(2,85 = \frac{1}{{10}}x + 1 \Leftrightarrow x = 18,5\,{\rm{(m)}}\).
Vậy người thợ lặn ở độ sâu 18,5 m thì chịu được áp suất 2,85 atm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
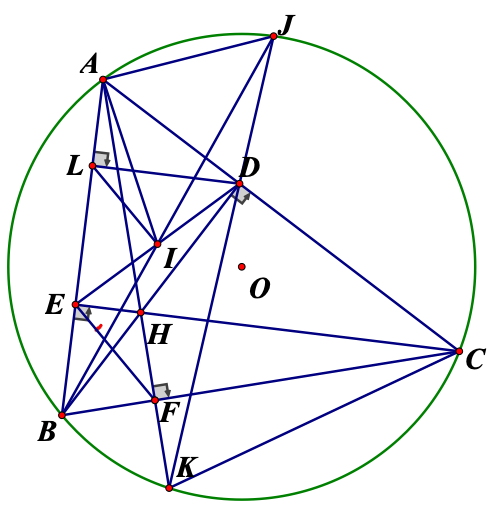
a) \(\widehat {BEC} = \widehat {BDC} = 90^\circ \)(\(BD,CE\)là hai đường cao của tam giác \(ABC)\)
\( \Rightarrow \)tứ giác \(BEDC\)nội tiếp (2 đỉnh liên tiếp cùng nhìn \(BC\))
Tam giác \(BDA\)vuông tại D có DL là đường cao nên \(B{D^2} = BL.BA\)
b) \(\widehat {BJK} = \widehat {BAK}\) (cùng chắn
\(\widehat {BAK} = \widehat {BCE}\) (cùng phụ \(\widehat {ABC})\)
\(\widehat {BCE} = \widehat {BDE}\) (cùng chắn
Vậy \(\widehat {BJK} = \widehat {BDE}\).
c) Gọi \(I\) là giao điểm của \(BJ\)và \(ED\)
\( \Rightarrow \widehat {BLI} = \widehat {BJA} \Rightarrow ALIJ\)là tứ giác nội tiếp
Chứng minh \(I\) là trung điểm của \(DE\)
\(\widehat {DLI} = \widehat {IDL}\)(cùng phụ hai góc bằng nhau )\( \Rightarrow ID = IL\)
Vậy \(I\) là trung điểm của \(ED.\)
Lời giải
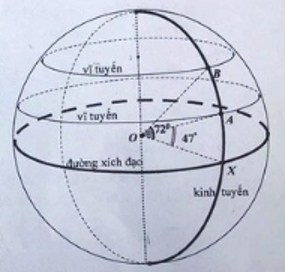
a) Khoảng cách giữa hai vị trí đó: \(\frac{{20000}}{{180}}.\left( {72 - 47} \right) \approx 2777,78\,\,{\rm{(km)}}\).
b) Bán kính của trái đất: \(\frac{{20000}}{{3,14}} \approx 6369,43\,\,{\rm{(km)}}\)
Độ dài đường xích đạo: \(20000:2 = 10000(km)\)
Thể tích trái đất: \(\frac{4}{3}.3,14.{\left( {6369,43} \right)^3} = 1,08\,{.10^{12}}\,{\rm{(k}}{{\rm{m}}^{\rm{3}}}{\rm{)}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.