Một nhóm gồm 31 bạn học sinh tổ chức một chuyến đi du lịch (chi phí chuyến đi được chia đều cho mỗi bạn tham gia). Sau khi đã hợp đồng xong, vào giờ chót có 3 bạn bận việc đột xuất không đi được nên họ không đóng tiền. Cả nhóm thống nhất mỗi bạn còn lại sẽ đóng thêm 18 000 đồng so với dự kiến ban đầu để bù lại cho 3 bạn không tham gia. Hỏi tổng chi phí chuyến đi là bao nhiêu?
Một nhóm gồm 31 bạn học sinh tổ chức một chuyến đi du lịch (chi phí chuyến đi được chia đều cho mỗi bạn tham gia). Sau khi đã hợp đồng xong, vào giờ chót có 3 bạn bận việc đột xuất không đi được nên họ không đóng tiền. Cả nhóm thống nhất mỗi bạn còn lại sẽ đóng thêm 18 000 đồng so với dự kiến ban đầu để bù lại cho 3 bạn không tham gia. Hỏi tổng chi phí chuyến đi là bao nhiêu?
Quảng cáo
Trả lời:
Cách 1:
Gọi số tiền mỗi bạn đóng ban đầu là \(x\)(đồng) \(\left( {x > 0} \right)\).
Số tiền mà 31 bạn phải đóng là \(31x\) (đồng).
Vào giờ chót, còn lại số bạn đi được là: 31 – 3 = 28 (bạn).
Số tiền mỗi bạn phải đóng sau khi tăng là \(x + 18\,000\) (đồng).
Chi phí chuyến đi của 28 bạn lúc sau là \(28\left( {x + 18\,000} \right)\).
Vì chi phí chuyến đi là không đổi nên ta có phương trình:
\(31x = 28\left( {x + 18\,000} \right)\)
\( \Leftrightarrow 31x - 28x = 28.18\,000\)
\( \Leftrightarrow 3x = 504\,000\)
\( \Leftrightarrow x = 168\,000\).
Vậy chi phí chuyến đi là: 31 . 168 000 = 5 208 000 đồng.
Cách 2:
Số tiền phải đóng bù cho 3 bạn: \(\left( {31 - 3} \right).18000 = 504000\)(đồng)
Tổng chi phí cho chuyến đi: \(\frac{{504000}}{3}.31 = 5208000\)(đồng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
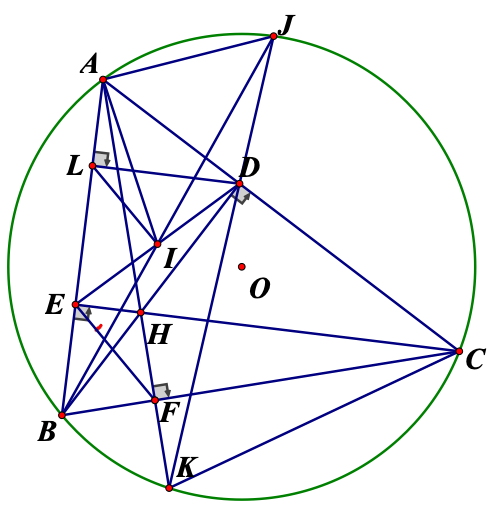
a) \(\widehat {BEC} = \widehat {BDC} = 90^\circ \)(\(BD,CE\)là hai đường cao của tam giác \(ABC)\)
\( \Rightarrow \)tứ giác \(BEDC\)nội tiếp (2 đỉnh liên tiếp cùng nhìn \(BC\))
Tam giác \(BDA\)vuông tại D có DL là đường cao nên \(B{D^2} = BL.BA\)
b) \(\widehat {BJK} = \widehat {BAK}\) (cùng chắn
\(\widehat {BAK} = \widehat {BCE}\) (cùng phụ \(\widehat {ABC})\)
\(\widehat {BCE} = \widehat {BDE}\) (cùng chắn
Vậy \(\widehat {BJK} = \widehat {BDE}\).
c) Gọi \(I\) là giao điểm của \(BJ\)và \(ED\)
\( \Rightarrow \widehat {BLI} = \widehat {BJA} \Rightarrow ALIJ\)là tứ giác nội tiếp
Chứng minh \(I\) là trung điểm của \(DE\)
\(\widehat {DLI} = \widehat {IDL}\)(cùng phụ hai góc bằng nhau )\( \Rightarrow ID = IL\)
Vậy \(I\) là trung điểm của \(ED.\)
Lời giải
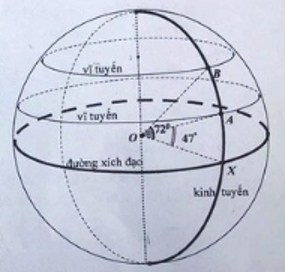
a) Khoảng cách giữa hai vị trí đó: \(\frac{{20000}}{{180}}.\left( {72 - 47} \right) \approx 2777,78\,\,{\rm{(km)}}\).
b) Bán kính của trái đất: \(\frac{{20000}}{{3,14}} \approx 6369,43\,\,{\rm{(km)}}\)
Độ dài đường xích đạo: \(20000:2 = 10000(km)\)
Thể tích trái đất: \(\frac{4}{3}.3,14.{\left( {6369,43} \right)^3} = 1,08\,{.10^{12}}\,{\rm{(k}}{{\rm{m}}^{\rm{3}}}{\rm{)}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.