Cho tam giác \(ABC\)\(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Hai đường cao \(BD\) và \(CE\) của tam giác \(ABC\) cắt nhau tại \(H\). Đường thẳng \(AH\) cắt \(BC\) và \(\left( O \right)\) lần lượt tại \(F\) và \(K\) \(\left( {K \ne A} \right).\)Gọi \(L\) là hình chiếu của \(D\) lên \(AB\).
a) Chứng minh rằng tứ giác \(BEDC\) nội tiếp và \(B{D^2} = BL.BA\).
b) Gọi \(J\) là giao điểm của \(KD\) và \(\left( O \right)\), \(\left( {J \ne K} \right).\) Chứng minh \(\widehat {BJL} = \widehat {BDE}\).
c) Gọi \(I\) là giao điểm của \(BJ\) và \(ED.\) Chứng minh tứ giác \(ALIJ\)nội tiếp và \(I\) là trung điểm của \(ED.\)
Cho tam giác \(ABC\)\(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Hai đường cao \(BD\) và \(CE\) của tam giác \(ABC\) cắt nhau tại \(H\). Đường thẳng \(AH\) cắt \(BC\) và \(\left( O \right)\) lần lượt tại \(F\) và \(K\) \(\left( {K \ne A} \right).\)Gọi \(L\) là hình chiếu của \(D\) lên \(AB\).
a) Chứng minh rằng tứ giác \(BEDC\) nội tiếp và \(B{D^2} = BL.BA\).
b) Gọi \(J\) là giao điểm của \(KD\) và \(\left( O \right)\), \(\left( {J \ne K} \right).\) Chứng minh \(\widehat {BJL} = \widehat {BDE}\).
c) Gọi \(I\) là giao điểm của \(BJ\) và \(ED.\) Chứng minh tứ giác \(ALIJ\)nội tiếp và \(I\) là trung điểm của \(ED.\)
Quảng cáo
Trả lời:
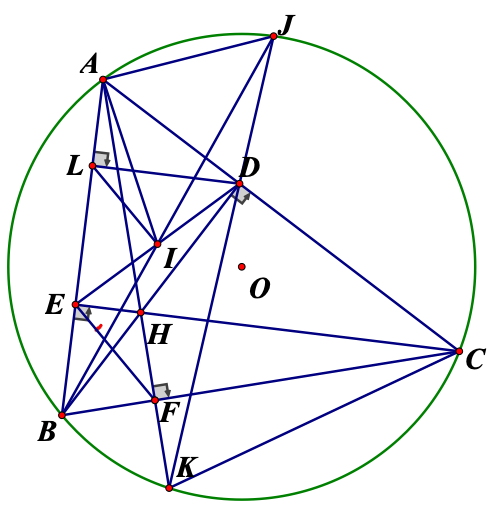
a) \(\widehat {BEC} = \widehat {BDC} = 90^\circ \)(\(BD,CE\)là hai đường cao của tam giác \(ABC)\)
\( \Rightarrow \)tứ giác \(BEDC\)nội tiếp (2 đỉnh liên tiếp cùng nhìn \(BC\))
Tam giác \(BDA\)vuông tại D có DL là đường cao nên \(B{D^2} = BL.BA\)
b) \(\widehat {BJK} = \widehat {BAK}\) (cùng chắn
\(\widehat {BAK} = \widehat {BCE}\) (cùng phụ \(\widehat {ABC})\)
\(\widehat {BCE} = \widehat {BDE}\) (cùng chắn
Vậy \(\widehat {BJK} = \widehat {BDE}\).
c) Gọi \(I\) là giao điểm của \(BJ\)và \(ED\)
\( \Rightarrow \widehat {BLI} = \widehat {BJA} \Rightarrow ALIJ\)là tứ giác nội tiếp
Chứng minh \(I\) là trung điểm của \(DE\)
\(\widehat {DLI} = \widehat {IDL}\)(cùng phụ hai góc bằng nhau )\( \Rightarrow ID = IL\)
Vậy \(I\) là trung điểm của \(ED.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
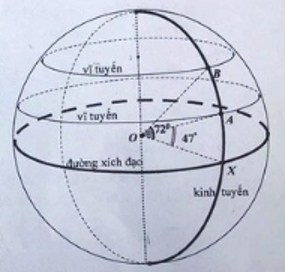
a) Khoảng cách giữa hai vị trí đó: \(\frac{{20000}}{{180}}.\left( {72 - 47} \right) \approx 2777,78\,\,{\rm{(km)}}\).
b) Bán kính của trái đất: \(\frac{{20000}}{{3,14}} \approx 6369,43\,\,{\rm{(km)}}\)
Độ dài đường xích đạo: \(20000:2 = 10000(km)\)
Thể tích trái đất: \(\frac{4}{3}.3,14.{\left( {6369,43} \right)^3} = 1,08\,{.10^{12}}\,{\rm{(k}}{{\rm{m}}^{\rm{3}}}{\rm{)}}\).
Lời giải
Vì \(ac = 2.\left( { - 1} \right) = - 2 < 0\) nên phương trình đã cho có hai nghiệm phân biệt.
Ta có: \({x_1},\,\,{x_2} \ne - 1\) vì \(2.{\left( { - 1} \right)^3} - 3.\left( { - 1} \right) - 1 = 4 \ne 0\).
Theo Vi-ét, ta có: \({x_1} + {x_2} = \frac{3}{2}; & {x_1}{x_2} = - \frac{1}{2}\).
\(A = \frac{{{x_1} - 1}}{{{x_2} + 1}} + \frac{{{x_2} - 1}}{{{x_1} + 1}} = \frac{{\left( {{x_1} - 1} \right)\left( {{x_1} + 1} \right) + \left( {{x_2} - 1} \right)\left( {{x_2} + 1} \right)}}{{\left( {{x_2} + 1} \right)\left( {{x_1} + 1} \right)}}\)
\( = \frac{{x_1^2 + x_2^2 - 2}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} - 2}}{{{x_1}{x_2} + \left( {{x_1} + {x_2}} \right) + 1}} = \frac{5}{8}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.