Cho \(a,\,\,b,\,\,c\) là các số không âm thỏa mãn \(a + b + c = 3\). Chứng minh rằng

\(\sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  + \sqrt {6b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  + \sqrt {6c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le 6\sqrt 2 \).

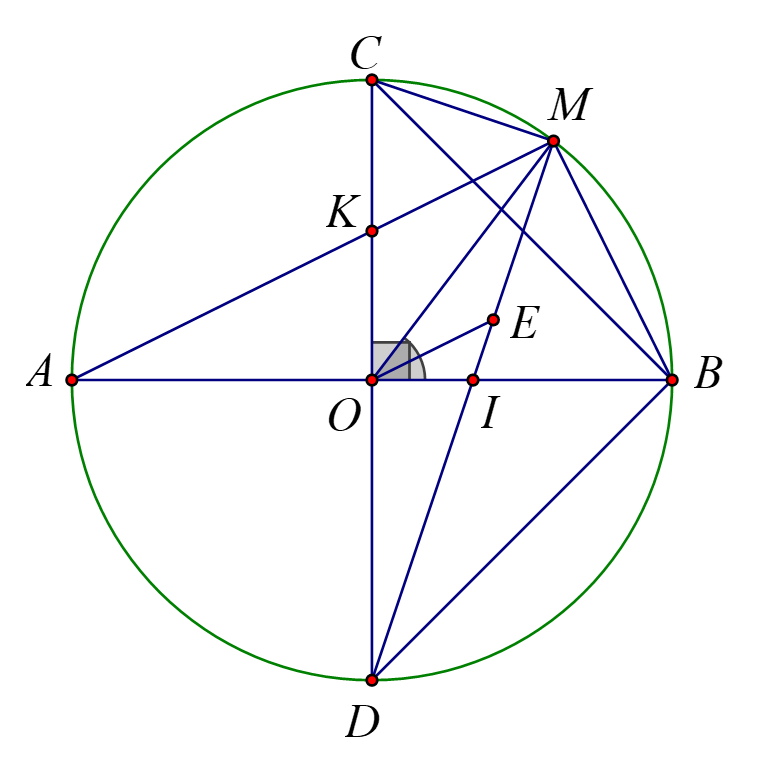
a) Chứng minh tứ giác \(OBMK\) nội tiếp.

\(\widehat {KMB} = \widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đương tròn)

\(\widehat {KOB} = 90^\circ \) (vì hai đường kính \(AB\) và \(CD\) vuông góc với nhau)

Do đó tam giác \(BMK\) và tam giác \(OBK\) nội tiếp đường tròn đường kính \(BM\)

Suy ra bốn điểm \(B\), \(O\), \(M\), \(K\) thuộc đường tròn đường kính \(BK\).

Vậy tứ giác \(OBMK\) nội tiếp đường tròn đường kính \(BK\).

b) Chứng minh rằng \(DI.DM = 2{R^2}\).

\(\widehat {CMD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Xét tam giác \(OID\) vuông tại \(O\) và tam giác \(MCD\) vuông tại \(M\) có \(\widehat {CDM}\) chung

Suy ra  (g.g)

Nên \[\frac{{DI}}{{DC}} = \frac{{DO}}{{DM}}\]

Do đó \(DI.DM = 2R.R = 2{R^2}\)

c) Tia phân giác của góc \(IOM\)cắt \(MI\) tại điểm \(E\). Chứng minh rằng \(\tan \widehat {ODI} = \frac{{EI}}{{EM}}\).

Xét tam giác \(OMI\) có \(OE\) là tia phân giác \(\widehat {MOI}\) nên \[\frac{{EI}}{{EM}} = \frac{{OI}}{{OM}}\,\,\,\left( 1 \right)\]

Xét tam giác \(OID\) vuông tại \(O\) nên \(\tan \widehat {ODI} = \frac{{OI}}{{OD}} = \frac{{OI}}{{OM}}\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta suy ra: \(\tan \widehat {ODI} = \frac{{EI}}{{EM}}\)

d) Cho \(IB = 2.IO\). Tính tỉ số \(\frac{{MB}}{{MC}}\).

Ta có  (theo câu b)

Suy ra \[\frac{{IO}}{{MC}} = \frac{{DO}}{{MD}}\] nên \[MC = \frac{{IO.MD}}{{DO}}\,\,\,\left( 3 \right)\]

Xét tam giác \(DIB\) và tam giác \(DBM\) có

\(\widehat {BDM}\): góc chung

\(\widehat {IBD} = \widehat {BMD}\) (2 góc nội tiếp chắn hai cung \(AD\) và \(BD\) bằng nhau của \(\left( O \right)\))

Suy ra  (g.g)

Nên \[\frac{{IB}}{{BM}} = \frac{{DB}}{{MD}}\]

Do đó \[MB = \frac{{IB.MD}}{{DB}}\,\,\,\left( 4 \right)\]

Từ (3) và (4) ta suy ra: \(\frac{{MB}}{{MC}} = \frac{{IB.MD}}{{DB}} \cdot \frac{{DO}}{{IO.MD}} = \frac{{2IO.R}}{{IO.R\sqrt 2 }} = \sqrt 2 \).

Suy ra \( - 8 = a.\,\,{3^2}\) hay \(a = \frac{{ - 8}}{9}\) (thoả mãn a < 0).

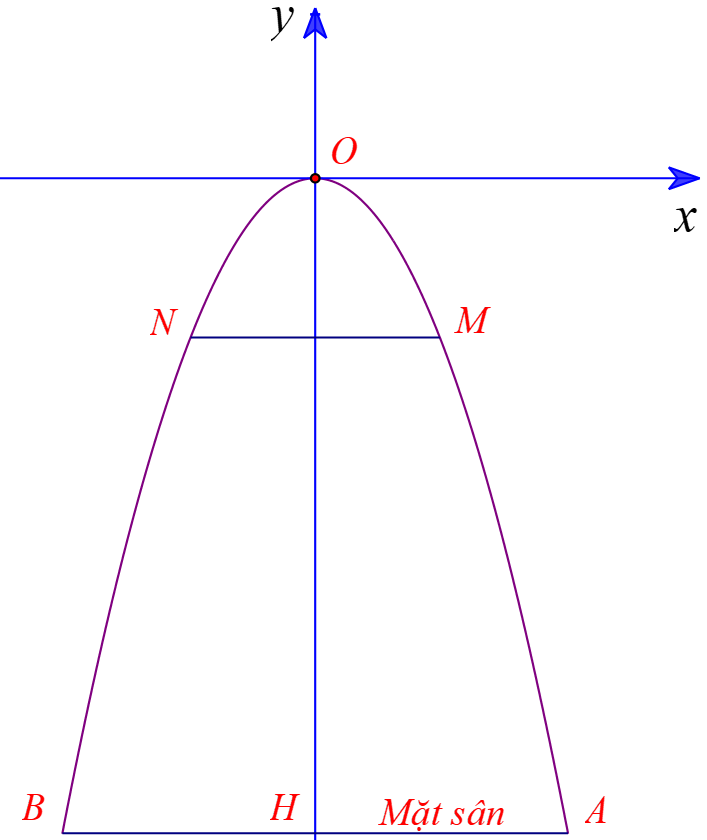
Phương trình parabol là: \(y =  - \frac{8}{9}{x^2}\)

Vì \(MN = 3\,\,m\) nên hoành độ điểm M là \({x_M} = \frac{3}{2}\) suy ra tung độ của M:\({y_M} =  - \frac{8}{9}.\,\,{\left( {\frac{3}{2}} \right)^2} =  - 2\).

Khoảng cách từ dây đèn đến mặt sân bằng \(8 - 2 = 6\,\,\left( m \right)\)