Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Bạc Liêu năm học 2025-2026 có đáp án

a) Tính giá trị của biểu thức \[B\] khi \[x = 9\]         .

Với \[x = 9\] thỏa điều kiện \[x \ge 0,\,x \ne 16\] nên ta có:

\(B = \frac{{9 - \sqrt 9  + 4}}{{\sqrt 9  - 4}} = \frac{{9 - 3 + 4}}{{3 - 4}} = \frac{{10}}{{ - 1}} =  - 10\)

Vậy khi \[x = 9\] thì \(B =  - 10\).

b) Chứng minh rằng \(A = \frac{{\sqrt x }}{{\sqrt x  - 4}}\)  .

Với \[x \ge 0,\,x \ne 16\], ta có:

\(A = \frac{{6\sqrt x  - 8}}{{x - 16}} + \frac{{\sqrt x }}{{\sqrt x  + 4}} + \frac{2}{{\sqrt x  - 4}}\)

\(A = \frac{{6\sqrt x  - 8}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} + \frac{{\sqrt x }}{{\sqrt x  + 4}} + \frac{2}{{\sqrt x  - 4}}\)

\(A = \frac{{6\sqrt x  - 8}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} + \frac{{\sqrt x \left( {\sqrt x  - 4} \right)}}{{\sqrt x  + 4}} + \frac{{2\left( {\sqrt x  + 4} \right)}}{{\sqrt x  - 4}}\)

\(A = \frac{{6\sqrt x  - 8 + x - 4\sqrt x  + 2\sqrt x  + 8}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}}\)

\(A = \frac{{\sqrt x \left( {\sqrt x  + 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}}\)

\(A = \frac{{\sqrt x }}{{\sqrt x  - 4}}\)

Vậy với \[x \ge 0,\,x \ne 16\] thì \(A = \frac{{\sqrt x }}{{\sqrt x  - 4}}\).

 c) Đặt \[P = \frac{A}{B}\]. Tìm giá trị lớn nhất của biểu thức \[P\].

 Với \[x \ge 0,\,x \ne 16\], ta có:

\[P = \frac{A}{B} = \frac{{\sqrt x }}{{\sqrt x  - 4}}:\frac{{x - \sqrt x  + 4}}{{\sqrt x  - 4}} = \frac{{\sqrt x }}{{\sqrt x  - 4}} \cdot \frac{{\sqrt x  - 4}}{{x - \sqrt x  + 4}} = \frac{{\sqrt x }}{{x - \sqrt x  + 4}}\]

* Với \[x = 0\], ta có: \[P = \frac{{\sqrt 0 }}{{0 - \sqrt 0  + 4}} = 0\,\,\left( 1 \right)\]

* Với \[x > 0,\,x \ne 16\], ta có:

\[P = \frac{{\sqrt x }}{{x - \sqrt x  + 4}} = \frac{1}{{\sqrt x  - 1 + \frac{4}{{\sqrt x }}}}\]

Áp dụng bất đẳng thức Cauchy cho hai số dương \[\sqrt x \] và \[\frac{4}{{\sqrt x }}\], ta có:

\[\begin{array}{l}\sqrt x  + \frac{4}{{\sqrt x }} \ge 4\\\sqrt x  - 1 + \frac{4}{{\sqrt x }} \ge 3\\\frac{1}{{\sqrt x  - 1 + \frac{4}{{\sqrt x }}}} \le \frac{1}{3}\end{array}\].

Hay \[P \le \frac{1}{3}\,\,\left( 2 \right)\]

Dấu  xảy ra khi \[\sqrt x  = \frac{4}{{\sqrt x }}\] hay \[x = 4\] (thỏa mãn)

Từ \[\left( 1 \right);\,\,\left( 2 \right)\] ta có \[{P_{\max }} = \frac{1}{3}\,\,\]khi \[x = 4\].

Vậy giá trị lớn nhất của \[P\] bằng \[\frac{1}{3}\], đạt được tại \[x = 4\].

                Không gian mẫu \(\Omega  = \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8;\,\,9;\,\,10;\,\,11;\,\,12} \right\}\)

Số phần tử của tập \(\Omega \) là \(12\).

Các kết quả thuận lợi cho biến cố A là : \(3,\,\,6,\,\,9,\,\,12\). Có \(4\)kết quả.

Xác suất của biến cố A là \(P\left( A \right) = \frac{4}{{12}} = \frac{1}{3}\).

Theo bài ra thể tích nước dâng lên bằng thể tích viên bi sắt nên ta có:

                \(\pi .\,\,{R^2}.\,\,x = 36\pi \)

                \(\pi .\,\,{\left( {3\sqrt 2 } \right)^2}.\,\,x = 36\pi \)

                 \(x = 2\,\,\left( {cm} \right)\).

Vậy \(x = 2\,\,\left( {cm} \right)\)

Số cuốn sách ở ngăn II lúc đầu là: \(y\) cuốn \(\left( {y \in N;\,\,y > 0} \right)\)

Số cuốn sách ở ngăn I nhiều hơn số cuốn sách ở ngăn II là \(100\) cuốn nên ta có phương trình: \(x - y = 100\,\,\left( 1 \right)\).

Chuyển \(25\% \) số cuốn sách ở ngăn I sang ngăn II thì số cuốn sách ở ngăn I bằng \(75\% \) số cuốn sách ở ngăn II nên ta có phương trình:

 \(\frac{{75}}{{100}}x = \frac{{75}}{{100}}\left( {y + \frac{{25}}{{100}}x} \right)\) hay \(y = \frac{3}{4}x\,\,\left( 2 \right)\)

Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình \(\left\{ \begin{array}{l}x - y = 100\\y = \frac{3}{4}x\end{array} \right.\)

Giải hệ trên ta được \(\left\{ \begin{array}{l}x = 400\\y = 300\end{array} \right.\) (thoả mãn điều kiện)

Vậy số cuốn sách ở ngăn I lúc đầu là 400 cuốn.

Số cuốn sách ở ngăn II lúc đầu là 300 cuốn.

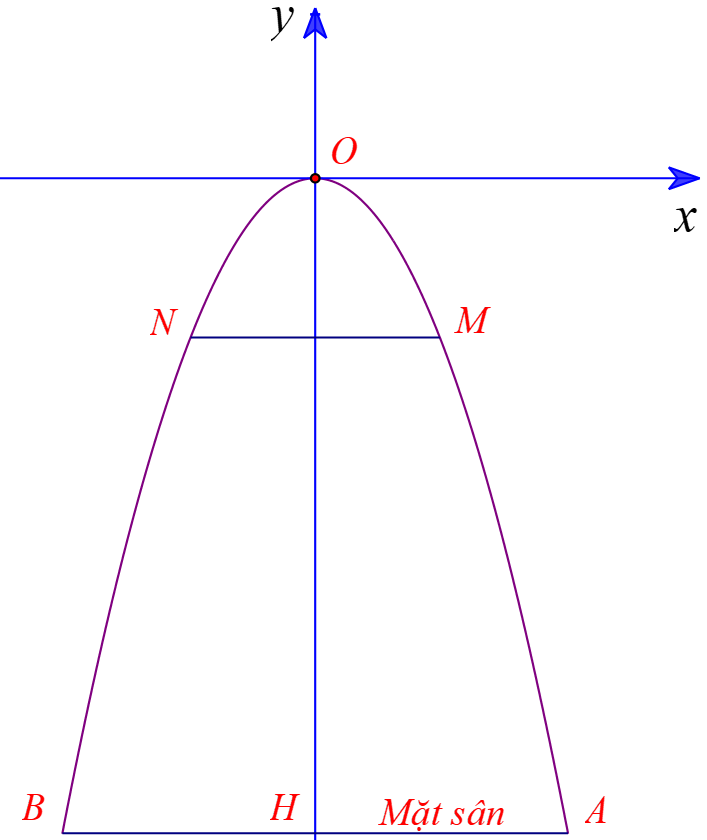
Suy ra \( - 8 = a.\,\,{3^2}\) hay \(a = \frac{{ - 8}}{9}\) (thoả mãn a < 0).

Phương trình parabol là: \(y =  - \frac{8}{9}{x^2}\)

Vì \(MN = 3\,\,m\) nên hoành độ điểm M là \({x_M} = \frac{3}{2}\) suy ra tung độ của M:\({y_M} =  - \frac{8}{9}.\,\,{\left( {\frac{3}{2}} \right)^2} =  - 2\).

Khoảng cách từ dây đèn đến mặt sân bằng \(8 - 2 = 6\,\,\left( m \right)\)