Câu hỏi:

09/04/2021 514

Cho parabol (P): $y = \frac{1}{4} x^{2}$ và đường thẳng d: $y = \frac{11}{8} x - \frac{3}{2}$ . Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất.

A. C( $\frac{3}{2}$ ; 0)

B. C(0; $\frac{3}{2}$ )

C. C( $\frac{1}{2}$ ; 0)

D. C(0; - $\frac{3}{2}$ )

Xem lời giải

Câu hỏi trong đề: 61 câu Trắc nghiệm Toán 9: Ôn tập chương IV có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án B

Hoành độ của A và B là nghiệm của phương trình $\frac{1}{4} x^{2} = \frac{11}{8} x - \frac{3}{2}$

Phương trình này có hai nghiệm: x = 4 và x = $\frac{3}{2}$

Suy ra A(4; 4), B( $\frac{3}{2}; \frac{9}{16}$ )

Dễ thấy hai điểm A, B cùng nằm về một phía so với trục tung (do cùng có hoành độ dương).

Lấy điểm A’( −4; 4) đối xứng với A qua trục tung

Khi đó CA + CB = CA’ + CB $\geq$ A’B, nên CA + CB đạt giá trị nhỏ nhất khi và chỉ khi A’, C, B thẳng hàng, tức là khi C là giao điểm của đường thẳng A’B với trục tung.

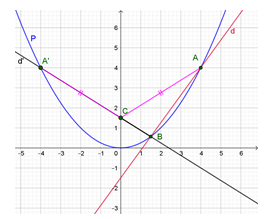
Phương trình đường thẳng d’ đi qua A’ và B có dạng y = ax + b

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho Parabol (P): y = $x^{2}$ và đường thẳng (d): y = mx + 4. Biết đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt A, B. Gọi $x_{1}; x_{2}$ là hoành độ của các điểm A, B. Tìm giá trị lớn nhất của $Q = \frac{2 (x_{1} + x_{2}) + 7}{{x_{1}}^{2} + {x_{2}}^{2}}$

A. −1

B. $\frac{- 1}{2}$

C. 1

D. $\frac{1}{4}$

Lời giải

Đáp án C

Phương trình hoành độ giao điểm của (d) và (P) là: $x^{2}$ = mx + 4 <=> $x^{2}$ − mx − 4 = 0. Ta có $∆$ = $m^{2}$ + 16 > 0, với mọi m nên phương trình luôn có 2 nghiệm phân biệt, suy ra đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt.

Suy ra giá trị lớn nhất của Q là 1 khi m = 1

Câu 2

Gọi $x_{A}, x_{B}$ là hoành độ của A và B. Tìm giá trị nhỏ nhất của biểu thức $T = \frac{4}{x_{A} + x_{B}} + \frac{1}{x_{A} . x_{B}}$

A. $\sqrt{2}$ + 1

B. 2

C. 2 $\sqrt{2}$

D. $\sqrt{2}$

Lời giải

Câu 3

Cho phương trình $x^{2}$ – (m + 1)x – 3 = 0 (1), với x là ẩn, m là tham số. Gọi $x_{1}; x_{2}$ là hai nghiệm của phương trình (1). Đặt B = $\frac{3 x_{1}^{2} + 3 x_{2}^{2} + 4 x_{1} + 4 x_{2} - 5}{x_{1}^{2} + x_{2}^{2} - 4}$ . Tìm m khi B đạt giá trị lớn nhất.

A. $\frac{- 1}{2}$

B. −1

C. 2

D. $\frac{1}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Hệ phương trình $\{\begin{cases} x^{2} y + {xy}^{2} = 6 \\ xy + x + y = 5 \end{cases}$

A. Có 2 nghiệm (5; 1) và (1; 5)

B. Có 2 nghiệm (2; 1) và (1; 2)

C. Có 1 nghiệm là (2; 2)

D. Có 4 nghiệm (1; 2); (2; 1); (1; 5) và (5; 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = $x^{2}$ và đường thẳng (d): $y = - \frac{2}{3} (m + 1) x + \frac{1}{3}$ (m là tham số). Trong trường hợp (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ giao điểm là $x_{1}; x_{2}$ . Đặt f (x) = $x^{3}$ + (m + 1) $x^{2}$ – x khi đó?

A. $f (x_{1}) - f (x_{2}) = {(x_{1} - x_{2})}^{3}$

B. $f (x_{1}) - f (x_{2}) = {\frac{1}{2} (x_{1} - x_{2})}^{3}$

C. $f (x_{1}) - f (x_{2}) = {- (x_{1} - x_{2})}^{3}$

D. $f (x_{1}) - f (x_{2}) = {- \frac{1}{2} (x_{1} - x_{2})}^{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Để hệ phương trình $\{\begin{cases} x + y = S \\ x . y = P \end{cases}$ có nghiệm, điều kiện cần và đủ là:

A. $S^{2}$ – P < 0

B. $S^{2}$ – P $\geq$ 0

C. $S^{2}$ – 4P < 0

D. $S^{2}$ – 4P $\geq$ 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong mặt phẳng Oxy cho đường thẳng (d): y = kx + $\frac{1}{2}$ và parabol (P): $y = \frac{1}{2} x^{2}$ . Giả sử đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Tọa độ trung điểm M của đoạn thẳng AB luôn thỏa mãn phương trình nào dưới đây?

A. y = $x^{2} + \frac{1}{2}$

B. y = $x^{2}$

C. y = $x + \frac{1}{2}$

D. y = $\frac{1}{2} x$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho parabol (P): y=14x2 và đường thẳng d: y=118x−32. Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất.

Bình luận

Cho Parabol (P): y = x2 và đường thẳng (d): y = mx + 4. Biết đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt A, B. Gọix1; x2 là hoành độ của các điểm A, B. Tìm giá trị lớn nhất của Q=2x1+x2+7x12+x22

Gọi xA, xB là hoành độ của A và B. Tìm giá trị nhỏ nhất của biểu thức T=4xA+xB+1xA.xB

Cho phương trình x2 – (m + 1)x – 3 = 0 (1), với x là ẩn, m là tham số. Gọi x1; x2 là hai nghiệm của phương trình (1). Đặt B = 3x12+3x22+4x1+4x2−5x12+x22−4. Tìm m khi B đạt giá trị lớn nhất.

Hệ phương trình x2y+xy2=6xy+x+y=5

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = x2 và đường thẳng (d): y=−23m+1x+13 (m là tham số). Trong trường hợp (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ giao điểm là x1; x2. Đặt f (x) = x3 + (m + 1)x2 – x khi đó?

Để hệ phương trình x+y=Sx.y=Pcó nghiệm, điều kiện cần và đủ là:

Trong mặt phẳng Oxy cho đường thẳng (d): y = kx + 12 và parabol (P): y=12x2. Giả sử đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Tọa độ trung điểm M của đoạn thẳng AB luôn thỏa mãn phương trình nào dưới đây?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho parabol (P): $y = \frac{1}{4} x^{2}$ và đường thẳng d: $y = \frac{11}{8} x - \frac{3}{2}$ . Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất.

Gọi $x_{A}, x_{B}$ là hoành độ của A và B. Tìm giá trị nhỏ nhất của biểu thức $T = \frac{4}{x_{A} + x_{B}} + \frac{1}{x_{A} . x_{B}}$

Cho phương trình $x^{2}$ – (m + 1)x – 3 = 0 (1), với x là ẩn, m là tham số. Gọi $x_{1}; x_{2}$ là hai nghiệm của phương trình (1). Đặt B = $\frac{3 x_{1}^{2} + 3 x_{2}^{2} + 4 x_{1} + 4 x_{2} - 5}{x_{1}^{2} + x_{2}^{2} - 4}$ . Tìm m khi B đạt giá trị lớn nhất.

Hệ phương trình $\{\begin{cases} x^{2} y + {xy}^{2} = 6 \\ xy + x + y = 5 \end{cases}$

Để hệ phương trình $\{\begin{cases} x + y = S \\ x . y = P \end{cases}$ có nghiệm, điều kiện cần và đủ là: