Câu hỏi:

12/07/2024 32,240

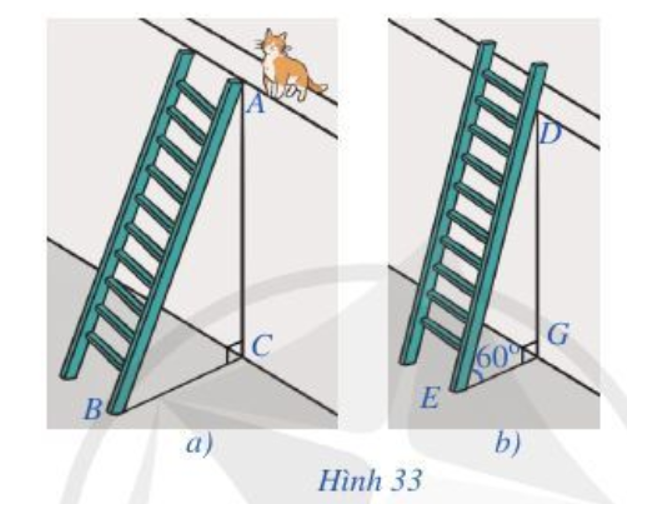
Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng và mép trên bức tường (Hình 33a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc 60° (Hình 33b). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Xem lời giải

Câu hỏi trong đề: Bài tập Hai dạng phương trình quy về phương trình bậc hai có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi chiều cao của bức tường là x (mét) (x > 0).

Vì chiếc thang cao hơn tường 1 m nên chiều cao của chiếc thang là x + 1 (m).

Khi đó quan sát Hình 33a ta thấy, AC = x, AB = x + 1, tam giác ABC vuông tại C, áp dụng định lý Pythagore ta có: AB² = AC² + BC²

Suy ra: BC² = AB² – AC² = (x + 1)² – x² = 2x + 1 $\Rightarrow B C = \sqrt{2 x + 1}$ (m).

Quan sát Hình 33b, ta thấy chiều cao bức tường không thay đổi nên DG = x (m).

Khi bác Nam dịch chuyển chân thang vào gần tường thêm 0,5 m thì GE = BC – 0,5.

Suy ra $G E = \sqrt{2 x + 1} - 0,5$ (m)

Lại có tam giác DGE vuông tại G nên ta có: $\tan \hat{D E G} = \frac{D G}{G E}$

Mà $\hat{D E G} = 60 °$ , DG = x, $G E = \sqrt{2 x + 1} - 0,5$

Do đó: $\frac{x}{\sqrt{2 x + 1} - 0,5} = \tan 60 ° = \sqrt{3}$

Suy ra: $x = \sqrt{3} (\sqrt{2 x + 1} - 0,5)$

$\Leftrightarrow x = \sqrt{3 (2 x + 1)} - \frac{\sqrt{3}}{2}$

$\Leftrightarrow \sqrt{3 (2 x + 1)} = x + \frac{\sqrt{3}}{2}$ (1)

Bình phương hai vế của (1) ta được: $3 (2 x + 1) = {(x + \frac{\sqrt{3}}{2})}^{2}$

$\Leftrightarrow 6 x + 3 = x^{2} + \sqrt{3} x + \frac{3}{4}$

$\Leftrightarrow x^{2} + (\sqrt{3} - 6) x - \frac{9}{4} = 0$

$\Leftrightarrow [\begin{array}{l} x = \frac{6 - \sqrt{3} + \sqrt{48 - 12 \sqrt{3}}}{2} \approx 4,7 \\ x = \frac{6 - \sqrt{3} - \sqrt{48 - 12 \sqrt{3}}}{2} \approx - 0,5 \end{array}$

Do x > 0 nên x ≈ 4,7 là giá trị thỏa mãn.

Vậy bức tường cao khoảng 4,7 m.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 5 km/h như Hình 35. Tính khoảng cách từ vị trí B đến M, biết thời gian người đó đi từ A đến C là 148 phút.

Xem đáp án

Lời giải

Đổi 148 phút = $\frac{37}{15}$ giờ.

Gọi khoảng cách từ vị trí B đến M là x (km, x > 0).

Khi đó ta có: AB = 4 km, BM = x km, BC = 7 km, MC = BC – BM = 7 – x (km).

Tam giác ABM vuông tại B, áp dụng định lý Pythagore ta có:

AM² = AB² + BM² = 4² + x² = 16 + x²

^{$\Rightarrow A M = \sqrt{16 + x^{2}}$}

Do đó khoảng cách từ vị trí A đến M là $\sqrt{16 + x^{2}}$ km và vận tốc chèo thuyền là 3 km/h nên thời gian chèo thuyền từ A đến M là $t_{1} = \frac{\sqrt{16 + x^{2}}}{3}$ (giờ).

Khoảng cách từ M đến C là 7 – x (km) và người đó đi bộ với vận tốc 5 km/h nên thời gian đi bộ từ M đến C là $t_{2} = \frac{7 - x}{5}$ (giờ).

Thời gian người đó đi từ A đến C chính bằng tổng thời gian người đó đi từ A đến M và từ M đến C nên ta có t₁ + t₂ = t = $\frac{37}{15}$ (giờ).

Khi đó ta có phương trình: $\frac{\sqrt{16 + x^{2}}}{3} + \frac{7 - x}{5} = \frac{37}{15}$ $\Leftrightarrow 5 \sqrt{16 + x^{2}} + 3. (7 - x) = 37$

$\Leftrightarrow 5 \sqrt{16 + x^{2}} = 16 + 3 x$ (1)

Bình phương cả hai vế của (1) ta được: 25.(16 + x²) = (16 + 3x)²

⇔ 400 + 25x² = 256 + 96x + 9x²

⇔ 16x² – 96x + 144 = 0

⇔ x = 3 (thỏa mãn điều kiện x > 0)

Vậy khoảng cách từ vị trí B đến vị trí M là 3 km.

Câu 2

Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34. Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.

Xem đáp án

Lời giải

Đổi: 300 m = 0,3 km; 800 m = 0,8 km; 7,2 phút = 0,12 giờ.

Gọi độ dài khoảng cách từ vị trí C đến D là x (km, x > 0).

Khi đó ta có: AC = 0,3 km; CD = x km; BC = 0,8 km; DB = BC – CD = 0,8 – x (km).

Lại có tam giác ACD vuông tại C, áp dụng định lý Pythagore ta có:

AD² = AC² + CD² = (0,3)² + x² = 0,09 + x²

$\Rightarrow A D = \sqrt{0,09 + x^{2}}$ (km)

Do đó khoảng cách từ vị trí A đến vị trí D là $\sqrt{0,09 + x^{2}}$ km, mà vận tốc chèo thuyền là 6 km/h và vận tốc dòng nước không đáng kể nên thời gian người đó chèo thuyền từ vị trí A đến vị trí D là $t_{1} = \frac{\sqrt{0,09 + x^{2}}}{6}$ (giờ).

Quãng đường từ vị trí D đến vị trí B là 0,8 – x (km) và vận tốc chạy bộ là 10 km/h nên thời gian người đó chạy bộ từ vị trí D đến vị trí B là $t_{2} = \frac{0,8 - x}{10}$ (giờ).

Tổng thời gian người đó chèo thuyền là t₁ + t₂ = t = 0,12 (giờ).

Khi đó ta có phương trình: $\frac{\sqrt{0,09 + x^{2}}}{6} + \frac{0,8 - x}{10} = 0,12$