Cho a→ , b→ là hai vectơ khác vectơ 0→ . Trong trường hợp nào thì đẳng thức sau đúng? a) |a→+b→|=|a→|+|b→| ; b) |a→+b→|=|a→−b→| .

a) Áp dụng công thức u→2=|u→|2 . Bình phương hai vế của đẳng phức |a→+b→|=|a→|+|b→| , ta được:|a→+b→|2=(|a→|+|b→|)2 ⇔(a→+b→)2=|a→|2+2|a→|.|b→|+|b→|2 ⇔a→2+2a→.b→+b→2=a→2+2|a→|.|b→|+b→2 ⇔a→.b→=|a→|.|b→| Mà a→.b→=|a→|.|b→|.cos(a→, b→) Do đó: |a→|.|b→|=|a→|.|b→|.cos(a→, b→)⇔cos(a→, b→)=1 Suy ra: (a→, b→)=0° hay hai vectơ a→ và b→ cùng hướng. Vậy đẳng thức a) đúng khi hai vectơ a→ và b→ cùng hướng. b) Bình phương hai vế của đẳng thức |a→+b→|=|a→−b→| , ta được: |a→+b→|2=|a→−b→|2 ⇔(a→+b→)2=(a→−b→)2 ⇔a→2+2a→.b→+b→2=a→2−2a→.b→+b→2 ⇔a→.b→=0⇔a→⊥b→ Vậy đẳng thức b) đúng khi hai vectơ a→và b→ vuông góc với nhau.

Câu hỏi:

13/07/2024 7,636

Cho $\vec{a}$ , $\vec{b}$ là hai vectơ khác vectơ $\vec{0}$ . Trong trường hợp nào thì đẳng thức sau đúng?

a) $| \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} |$ ;

b) $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$ .

Xem lời giải

Câu hỏi trong đề: Bài tập cuối chương V có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Áp dụng công thức ${\vec{u}}^{2} = {| \vec{u} |}^{2}$ .

Bình phương hai vế của đẳng phức $| \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} |$ , ta được: ${| \vec{a} + \vec{b} |}^{2} = {(| \vec{a} | + | \vec{b} |)}^{2}$

$\Leftrightarrow {(\vec{a} + \vec{b})}^{2} = {| \vec{a} |}^{2} + 2 | \vec{a} | . | \vec{b} | + {| \vec{b} |}^{2}$

$\Leftrightarrow {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2} = {\vec{a}}^{2} + 2 | \vec{a} | . | \vec{b} | + {\vec{b}}^{2}$

$\Leftrightarrow \vec{a} . \vec{b} = | \vec{a} | . | \vec{b} |$

Mà $\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | . c o s (\vec{a}, \vec{b})$

Do đó: $| \vec{a} | . | \vec{b} | = | \vec{a} | . | \vec{b} | . c o s (\vec{a}, \vec{b}) \Leftrightarrow c o s (\vec{a}, \vec{b}) = 1$

Suy ra: $(\vec{a}, \vec{b}) = 0 °$ hay hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.

Vậy đẳng thức a) đúng khi hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.

b) Bình phương hai vế của đẳng thức $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$ , ta được: ${| \vec{a} + \vec{b} |}^{2} = {| \vec{a} - \vec{b} |}^{2}$

$\Leftrightarrow {(\vec{a} + \vec{b})}^{2} = {(\vec{a} - \vec{b})}^{2}$

$\Leftrightarrow {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2} = {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$

$\Leftrightarrow \vec{a} . \vec{b} = 0 \Leftrightarrow \vec{a} ⊥ \vec{b}$

Vậy đẳng thức b) đúng khi hai vectơ $\vec{a}$ và $\vec{b}$ vuông góc với nhau.

Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một xe goòng được kéo bởi một lực $\vec{F}$ có độ lớn là 50 N, di chuyển theo quãng đường từ A đến B có chiều dài 200 m. Cho biết góc giữa $\vec{F}$ và $\vec{A B}$ là 30° và $\vec{F}$ được phân tích thành 2 lực $\vec{F_{1}}, \vec{F_{2}}$ (Hình 3). Tính công sinh bởi các lực $\vec{F}, \vec{F_{1}}$ và $\vec{F_{2}}$ .

Xem đáp án

Lời giải

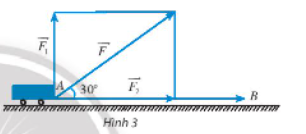
Công sinh bởi lực $\vec{F}$ là

A = $| \vec{F} | . A B . \cos (\vec{F}, \vec{A B})$ = 50 . 200 . cos30° = $5000 \sqrt{3}$ (J).

Góc tạo bởi lực $\vec{F_{1}}$ và $\vec{A B}$ là 90°, do đó công sinh bởi lực $\vec{F_{1}}$ là

A₁ = $| \vec{F_{1}} | . A B . \cos (\vec{F_{1}}, \vec{A B})$ = $| \vec{F_{1}} | .200. \cos 90 ° = 0$ (J).

Ta có: $| \vec{F_{2}} | = | \vec{F} | . \cos 30 ° = 50. \frac{\sqrt{3}}{2} = 25 \sqrt{3}$ (N)

Hai vectơ $\vec{F_{2}}$ và $\vec{A B}$ cùng hướng nên $(\vec{F_{2}}, \vec{A B}) = 0 °$ .

Do đó công sinh bởi lực $\vec{F_{2}}$ là

A₂ = $| \vec{F_{2}} | . A B . \cos (\vec{F_{2}}, \vec{A B})$ = $25 \sqrt{3} .200. \cos 0 ° = 5000 \sqrt{3}$ (J).

Câu 2

Một chiếc máy bay được biết là đang bay về phía bắc với tốc độ 45 m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc 20° về phía tây bắc (Hình 2). Tính tốc độ của gió.

Xem đáp án

Lời giải

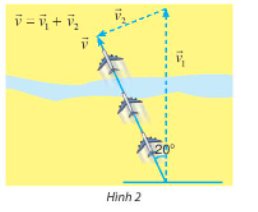
Quan sát Hình 2, ta thấy:

Vectơ vận tốc thực của máy bay là $\vec{v_{1}}$ và $| \vec{v_{1}} | = 45$ m/s.

Vectơ vận tốc gió là $\vec{v_{2}}$ , ta cần tính $| \vec{v_{2}} |$ .

Vectơ vận tốc của máy bay so với mặt đất là $\vec{v}$ và $| \vec{v} | = 38$ m/s.

Góc giữa hai vectơ $\vec{v}$ và $\vec{v_{1}}$ là 20°.

Ta có: $\vec{v} = \vec{v_{1}} + \vec{v_{2}} \Rightarrow \vec{v_{2}} = \vec{v} - \vec{v_{1}}$ (1)

Bình phương hai vế của (1), ta được:

${| \vec{v_{2}} |}^{2} = {(\vec{v} - \vec{v_{1}})}^{2}$

$\Leftrightarrow {| \vec{v_{2}} |}^{2} = {\vec{v}}^{2} - 2 \vec{v} . \vec{v_{1}} + {\vec{v_{1}}}^{2}$

$\Leftrightarrow {| \vec{v_{2}} |}^{2} = {| \vec{v} |}^{2} - 2. | \vec{v} | . | \vec{v_{1}} | . c o s (\vec{v}, \vec{v_{1}}) + {| \vec{v_{1}} |}^{2}$

$\Leftrightarrow {| \vec{v_{2}} |}^{2} = 38^{2} - 2 . 38 . 45 . c o s 20 ° + 45^{2}$

$\Leftrightarrow {| \vec{v_{2}} |}^{2} \approx 255, 25$

Suy ra: $| \vec{v_{2}} | \approx 15, 98$ .

Vậy tốc độ của gió khoảng 15,98 m/s.

Câu 3

Cho hình thoi ABCD có cạnh bằng a và có góc A bằng 60°. Tìm độ dài các vectơ sau: $\vec{p} = \vec{A B} + \vec{A D}$ ; $\vec{u} = \vec{A B} - \vec{A D}$ ; $\vec{v} = 2 \vec{A B} - \vec{A C}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên, dòng chảy của nước trên con sông đó chảy với tốc độ 1,20 m/s về hướng bên phải. Gọi $\vec{v_{1}}, \vec{v_{2}}, \vec{v}$ lần lượt là vận tốc của thuyền so với dòng nước, vận tốc của dòng nước so với bờ và vận tốc của thuyền so với bờ.

a) Tính độ dài của các vectơ $\vec{v_{1}}, \vec{v_{2}}, \vec{v}$ .

b) Tốc độ dịch chuyển của thuyền so với bờ là bao nhiêu?

c) Hướng di chuyển của thuyền lệch một góc bao nhiêu so với bờ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho $\vec{C E} = \vec{A N}$ (Hình 1).

a) Tìm tổng của các vectơ $\vec{N C}$ và $\vec{M C}$ ; $\vec{A M}$ và $\vec{C D}$ ; $\vec{A D}$ và $\vec{N C}$ .

b) Tìm các vectơ hiệu: $\vec{N C} - \vec{M C}; \vec{A C} - \vec{B C}; \vec{A B} - \vec{M E}$ .

c) Chứng minh $\vec{A M} + \vec{A N} = \vec{A B} + \vec{A D}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.

a) Tính độ dài của các vectơ $\vec{A C}, \vec{B D}$ .
b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng $\frac{a \sqrt{10}}{2}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tiếng Anh

Công nghệ

Tin học

ĐHQG Hà Nội

ĐHQG Hồ Chí Minh

ĐH Bách Khoa Hà Nội

ĐHSP Hà Nội

Bộ Công an

Bộ Quốc phòng

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý