Bài tập cuối chương V có đáp án
30 người thi tuần này 4.6 1.1 K lượt thi 12 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
a) Gọi Δ1, Δ2, Δ3 lần lượt là giá của ba vectơ .
+ Vectơ cùng phương với vectơ
⇒ Δ1 //≡ Δ3
+ Vectơ cùng phương với vectơ
⇒ Δ2 //≡ Δ3
Do đó: Δ1 //≡ Δ2
Vậy vectơ cùng phương với vectơ (theo định nghĩa).
Vậy khẳng định a) đúng.
b) Hai vectơ cùng ngược hướng với .
Suy ra đều cùng phương với .
Theo câu a suy ra vectơ cùng phương với vectơ .
Do đó, hai vectơ và chỉ có thể cùng hướng hoặc ngược hướng.
Mà hai vectơ và đều ngược hướng với nên hai vectơ và cùng hướng.
Vậy khẳng định b) đúng.
Lời giải
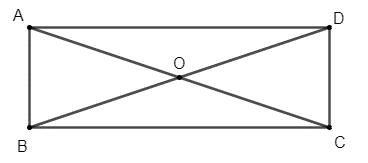
a) Vì ABCD là hình chữ nhật nên hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O.
Xét tam giác ABC vuông tại B, theo định lí Pythagore ta có:
AC2 = AB2 + BC2 = a2 + (3a)2 = 10a2 .
Do đó: BD = AC = .
Vậy .
b) Vì O là trung điểm của AC nên AO = OC = AC = .
Khi đó:
Hai vectơ và ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Hai vectơ và ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Vì O là trung điểm của BD nên BO = OD = BD = .
Khi đó: .
Hai vectơ và ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Hai vectơ và ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Vậy các cặp vectơ đối nhau và có độ dài bằng trong hình là: ; ; và .
Lời giải
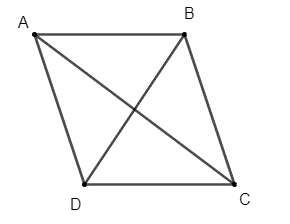
ABCD là hình thoi nên AB = BC = CD = DA = a.
Xét tam giác ABD có AB = AD và nên tam giác ABD đều.
Suy ra BD = AB = AD = a.
Ta có: .
Áp dụng định lí côsin trong tam giác ADC ta có:
AC2 = AD2 + DC2 – 2 . AD . DC . cosADC
= a2 + a2 – 2 . a . a . cos120° = 3a2
Suy ra: AC = .
+ Vì ABCD là hình thoi nên ABCD cũng là hình bình hành nên theo quy tắc hình bình hành ta có: .
Do đó: .
+ Ta có:
Do đó: .
+ Ta có:
Do đó: .
Lời giải
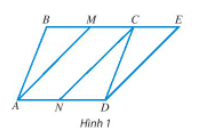
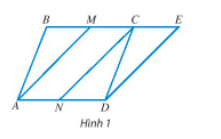
a) Vì ABCD là hình bình hành nên BC // = AD.
M và N lần lượt là trung điểm của BC và AD nên BM = MC = BC; AN = ND = AD
Mà nên CE //= AN.
Do đó: BM = MC = AN = ND = CE (1).
Hai vectơ và cùng hướng (do AN // MC và cùng hướng đi từ trái qua phải) và nên .
Khi đó ta có AMCN là hình bình hành nên .
Do đó:
Lại có: ME = MC + CE; AD = AN + ND (2)
Từ (1) và (2) suy ra ME = AD, mà ME // AD nên AMED là hình bình hành, theo quy tắc hình bình hành ta có: .
Do đó ta có: .
b) Vì và nên .
Vì ABCD là hình bình hành nên và .
Do đó ta có: .
Vì AMED là hình bình hành nên .
Do đó ta có: .
c) Do ABCD là hình bình hành nên .
Do AMCN là hình bình hành nên .
Từ đó suy ra: .
Lời giải
a) Áp dụng công thức .
Bình phương hai vế của đẳng phức , ta được:
Mà
Do đó:
Suy ra: hay hai vectơ và cùng hướng.
Vậy đẳng thức a) đúng khi hai vectơ và cùng hướng.
b) Bình phương hai vế của đẳng thức , ta được:
Vậy đẳng thức b) đúng khi hai vectơ và vuông góc với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.