Câu hỏi:
12/07/2024 803
Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ.
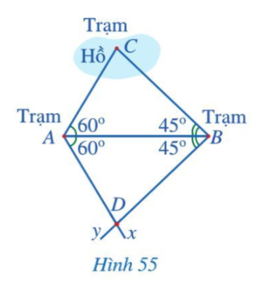
Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau (Hình 55):
- Đo góc BAC được 60o, đo góc ABC được 45o;
- Kẻ tia Ax sao cho , kẻ tia By sao cho , xác định giao điểm D của hai tia đó;
- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.
Tại sao lại có hai đẳng thức trên?
Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ.
Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau (Hình 55):
- Đo góc BAC được 60o, đo góc ABC được 45o;
- Kẻ tia Ax sao cho , kẻ tia By sao cho , xác định giao điểm D của hai tia đó;
- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.
Tại sao lại có hai đẳng thức trên?
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét và có:
.
AB chung.
Suy ra (g .c .g).
Do đó AC = AD (2 cạnh tương ứng) và BC = BD (2 cạnh tương ứng).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, , . Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, , . Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Xem đáp án »
13/07/2024
7,473
Câu 3:
Cho tam giác ABC có Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh .
b) Kẻ tia Dx nằm trong góc ADC sao cho . Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: , AB < AC.
Cho tam giác ABC có Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh .
b) Kẻ tia Dx nằm trong góc ADC sao cho . Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: , AB < AC.
Xem đáp án »
13/07/2024
5,066
Câu 6:
Cho . Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.
Cho . Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.
Xem đáp án »
13/07/2024
1,404
Câu 7:
Cho tam giác ABC (Hình 56).
Những góc nào của tam giác ABC có cạnh thuộc đường thẳng AB?
Trong tam giác ABC (Hình 56), ta gọi góc A và góc B là hai góc kề cạnh AB. Tương tự, góc B và góc C là hai góc kề cạnh BC, góc C và góc A là hai góc kề cạnh CA.
Cho tam giác ABC (Hình 56).
Những góc nào của tam giác ABC có cạnh thuộc đường thẳng AB?
Trong tam giác ABC (Hình 56), ta gọi góc A và góc B là hai góc kề cạnh AB. Tương tự, góc B và góc C là hai góc kề cạnh BC, góc C và góc A là hai góc kề cạnh CA.
Xem đáp án »
12/07/2024
1,183
về câu hỏi!