Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = g(x) thỏa mãn một trong hai bất phương trình f(x) ≥ 0 hoặc g(x) ≥ 0 mà không cần kiểm tra thỏa mãn đồng thời cả hai bất phương trình đó để kết luận nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \).
Quảng cáo
Trả lời:
Lời giải
Xét phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)(*)
Điều kiện tồn tại căn thức là: f(x) ≥ 0 hoặc g(x) ≥ 0
Bình phương hai vế của phương trình (*) ta được: f(x) = g(x).
Do đó ta chỉ cần hoặc f(x) ≥ 0 hoặc g(x) ≥ 0 là đủ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
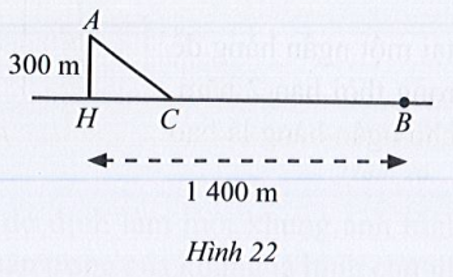
Đặt CH = x (x ≥ 0). Khi đó BC = 1 400 – x.
Xét tam giác AHC vuông tại H, có:
AH2 + HC2 = AC2
⇔ AC2 = 3002 + x2
⇔ AC = \(\sqrt {{x^2} + 90\,000} \)
Thời gian thuyền đi từ A đến C là: \(\frac{{\sqrt {{x^2} + 90\,000} }}{3}\) (giờ)
Thời gian người đi bộ đi từ B đến C là \(\frac{{1\,400 - x}}{6}\) (giờ)
Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C nên ta có:
\(\frac{{\sqrt {{x^2} + 90\,000} }}{3} = \,\frac{{1\,400 - x}}{6}\)
⇔ \(2\sqrt {{x^2} + 90\,000} = \,1400 - x\) (điều kiện x ≤ 1 400)
⇔ 4(x2 + 90 000) = 1 960 000 – 2 800x + x2
⇔ 3x2 + 2 800x – 1 600 000 = 0
⇔ x = 400 (TMĐK) hoặc x = \( - \frac{{4000}}{3}\) (không TMĐK)
⇒ CB = 1 400 – x = 1 400 – 400 = 1 000 (m).
Vậy khoảng cách CB = 1 000 m.
Lời giải
Lời giải
Đáp án đúng là D
Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.