Bộ 10 đề thi cuối kì 1 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 9
19 người thi tuần này 4.6 701 lượt thi 21 câu hỏi 60 phút
🔥 Đề thi HOT:
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
15 câu Trắc nghiệm Phép cộng hai số nguyên có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. \(M = \left\{ {7;\,\,8;\,\,9} \right\}.\)
B. \(M = \left\{ {6;\,\,7;\,\,8;\,\,9} \right\}.\)
C. \(M = \left\{ {7;\,\,8;\,\,9;\,\,10} \right\}.\)
D. \(M = \left\{ {6;\,\,7;\,\,8;\,\,9;\,\,10} \right\}.\)
Lời giải
Đáp án đúng là: D
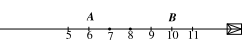
Đoạn \(AB\) bao gồm tất cả các số tự nhiên từ 6 đến 10, đó là các số \(6;\,\,7;\,\,8;\,\,9;\,\,10.\)
Vậy tập hợp \[M\] là \(M = \left\{ {6;\,\,7;\,\,8;\,\,9;\,\,10} \right\}.\)
Câu 2
A. \({a^m} + {a^n} = {a^{m\,\, \cdot \,\,n}}.\)
B. \({a^m} - {a^n} = {a^{m\,\,:\,\,n}}.\)
C. \({a^m} \cdot {a^n} = {a^{m\, + \,n}}.\)
D. \({a^m}:{a^n} = {a^{m\,\,\,:\,\,\,n}}.\)
Lời giải
Đáp án đúng là: C
Với hai số tự nhiên \(m,\,\,n\) thì \({a^m} \cdot {a^n} = {a^{m\, + \,n}}.\)
Câu 3
A. \(\left\{ {1;\,\,3;\,\,5;\,\,7} \right\}.\)
B. \(\left\{ {13;\,\,15;\,\,17;\,\,29} \right\}.\)
C. \(\left\{ {3;\,\,5;\,\,7;\,\,51} \right\}.\)
D. \(\left\{ {5;\,\,11;\,\,17;\,\,23} \right\}.\)
Lời giải
Đáp án đúng là: D
Số 1 không phải là số nguyên tố nên phương án A là sai.
Số 15 chia hết cho 3 và 5 nên không phải là số nguyên tố, do đó phương án B là sai.
Số 51 chia hết cho 3 và 17 nên không phải là số nguyên tố, do đó phương án C là sai.
Các số \(5;\,\,11;\,\,17;\,\,23\) chỉ chia hết cho 1 và chính nó nên là số nguyên tố.
Vậy ta chọn phương án D.
Câu 4
A. BCNN của \(a\) và \(b\) là số nhỏ nhất trong tập hợp bội chung của \(a\) và \(b.\)
B. BCNN\(\left( {a,\,\,b,\,\,1} \right) = \)BCNN\(\left( {a,\,\,b} \right).\)
C. Nếu \(m\,\, \vdots \,\,n\) thì BCNN\(\left( {m,\,\,n} \right) = n.\)
D. Nếu ƯCLN\(\left( {x,\,\,y} \right) = 1\) thì BCNN\(\left( {x,\,\,y} \right) = 1.\)
Lời giải
Đáp án đúng là: B
Ta có:
⦁ BCNN của \(a\) và \(b\) là số nhỏ nhất khác 0 trong tập hợp bội chung của \(a\) và \(b.\)
⦁ BCNN\(\left( {a,\,\,b,\,\,1} \right) = \)BCNN\(\left( {a,\,\,b} \right).\)
⦁ Nếu \(m\,\, \vdots \,\,n\) thì BCNN\(\left( {m,\,\,n} \right) = m.\)
⦁ Nếu ƯCLN\(\left( {x,\,\,y} \right) = 1\) thì BCNN\(\left( {x,\,\,y} \right) = xy.\)
Vậy ta chọn phương án B.
Câu 5
A. \( - 6 \in \mathbb{N}.\)
B. \( - 9 \notin \mathbb{Z}.\)
C. \( - 9 \in \mathbb{N}.\)
D. \( - 1 \in \mathbb{Z}.\)
Lời giải
Đáp án đúng là: D
Ta có: \( - 6 \notin \mathbb{N};\) \( - 9 \in \mathbb{Z};\) \( - 9 \notin \mathbb{N}\) và \( - 1 \in \mathbb{Z}.\)
Vậy ta chọn phương án D.
Câu 6
A. 10 m.
B. \( - 10\) m.
C. 50 m.
D. \( - 50\) m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 6.
B. 8.
C. 9.
D. 11.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
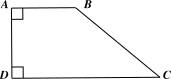
A. \(\left( {AB + CD} \right) \cdot AD.\)
B. \(\frac{{\left( {AB + CD} \right) \cdot AD}}{2}.\)
C. \(2\left( {AB + CD} \right) \cdot AD.\)
D. \(\frac{{AB \cdot CD \cdot AD}}{2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
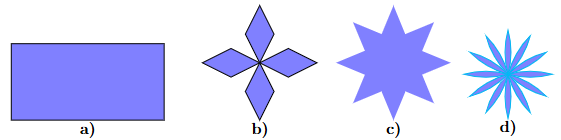
A. Hình tròn vừa có trục đối xứng vừa có tâm đối xứng.
B. Hình vuông có tâm đối xứng là giao điểm của hai đường chéo.
C. Hình chữ nhật vừa có trục đối xứng vừa có tâm đối xứng.
D. Hình bình hành vừa có trục đối xứng vừa có tâm đối xứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. Tính đối xứng chỉ thể hiện trong Toán học.
B. Tính đối xứng không thể hiện trong Sinh học.
C. Tính đối xứng không thể hiện trong Kiến trúc.
D. Tính đối xứng thể hiện trong Toán học, Tự nhiên, Kiến trúc, Nghệ thuật, Công nghệ chế tạo, ...
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.