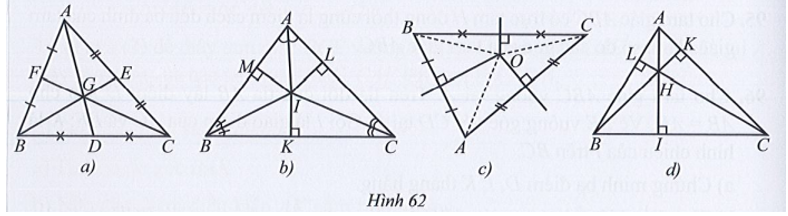
Trong các hình 62a, 62b, 62c, 62d, hình nào có điểm cách đều các đỉnh của tam giác đó? Vì sao?
Trong các hình 62a, 62b, 62c, 62d, hình nào có điểm cách đều các đỉnh của tam giác đó? Vì sao?
Câu hỏi trong đề: Giải SBT Toán 7 CD Bài tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
• Hình 62a:
Xét tam giác ABC có G là giao điểm của ba đường trung tuyến AD, BE, CF nên G là trọng tâm của tam giác ABC.
Do đó G không cách đều ba đỉnh của tam giác ABC
• Hình 62b:
Xét tam giác ABC có I là giao điểm của ba đường phân giác AI, BI, CI nên I cách đều ba cạnh của tam giác ABC.
Do đó I không cách đều ba đỉnh của tam giác ABC
• Hình 62c:
Xét tam giác ABC có O là giao điểm của ba đường trung trực nên OA = OB = OC.
Do đó O cách đều ba đỉnh của tam giác ABC.
• Hình 62d:
Xét tam giác ABC có H là giao điểm của ba đường cao AI, BK, CL nên H là trực tâm của tam giác ABC.
Do đó H không cách đều ba đỉnh của tam giác ABC.
Vậy hình 62c có điểm O cách đều các đỉnh của tam giác ABC.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Xét DAMC và DEMB có:
AM = ME (giả thiết),
(hai góc đối đỉnh),
BM = CM (vì M là trung điểm của BC)
Do đó ∆AMC = ∆EMB (c.g.c).
Suy ra AC = EB (hai cạnh tương ứng) và (hai góc tương ứng).
Mà và ở vị trí so le trong nên AC // BE.
Vậy AC = EB và AC song song với EB.
Lời giải
a) Xét DOHC và DOFC có:
,
OC là cạnh chung,
(do CO là tia phân giác của góc ACB).
Do đó ∆OHC = ∆OFC (cạnh huyền – góc nhọn).
suy ra CH = CF, OH = OF (các cặp cạnh tương ứng).
Do đó C và O cùng nằm trên đường trung trực của đoạn thẳng FH.
Hay CO là đường trung trực của đoạn thẳng FH.
Do đó OC ⊥ FH.
Vậy OC ⊥ FH.
Câu 3
A. 20°;
B. 30°;
C. 40°;
D. 50°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. AC = MP;
B. AB = MN;
C. BC = NP;
D. AC = MN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập