Dùng thước hai lề ta có thể dựng cặp đường thẳng song song với khoảng cách h không đổi.
Cho góc xOy. Dùng thước hai lề dựng cặp đường thẳng song song gồm đường thẳng chứa tia Ox và đường thẳng x’ (sao cho x’ cắt Oy) rồi dùng thước đo hai lề đó, dựng cặp đường thẳng song song gồm đường thẳng chứa tia Oy và đường thẳng y’ (sao cho y’ cắt Ox). Hai đường thẳng x’ và y’ cắt nhau tại P. Chứng minh rằng tia OP là tia phân giác của góc xOy.
Dùng thước hai lề ta có thể dựng cặp đường thẳng song song với khoảng cách h không đổi.
Cho góc xOy. Dùng thước hai lề dựng cặp đường thẳng song song gồm đường thẳng chứa tia Ox và đường thẳng x’ (sao cho x’ cắt Oy) rồi dùng thước đo hai lề đó, dựng cặp đường thẳng song song gồm đường thẳng chứa tia Oy và đường thẳng y’ (sao cho y’ cắt Ox). Hai đường thẳng x’ và y’ cắt nhau tại P. Chứng minh rằng tia OP là tia phân giác của góc xOy.
Quảng cáo
Trả lời:
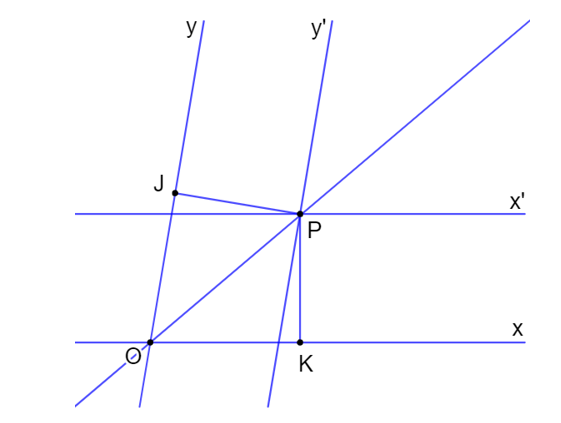
Do P thuộc đường thẳng x’ nên khoảng cách từ P đến x là PK và bằng h (vì x // x’) (1)
Do P thuộc đường thẳng y’ nên khoảng cách từ P đến y là PJ và bằng h (vì y // y’) (2)
Từ (1) và (2) suy ra: Khoảng cách từ P đến x bằng khoảng cách từ P đến y.
Hay điểm P cách đều hai đường thẳng x và y.
Do đó P nằm trên đường phân giác của góc xOy (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
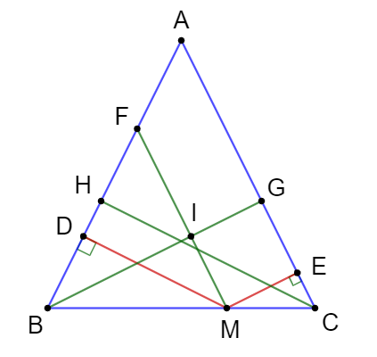
Gọi BG và CH là đường cao kẻ từ B và C của ∆ABC.
Gọi MD, ME lần lượt là khoảng cách từ M đến AB và AC.
Kẻ MF song song với cạnh AC (F ∈ AB).
MF giao với BG tại điểm I.
Tương tự cách làm của Bài 9.8 trong tam giác ABC cân tại A thì khoảng cách từ B đến AC bằng khoảng cách từ C đến AB. Ta dễ dàng suy ra được: BG = CH (4)
Tổng khoảng cách từ M đến AB và AC là MD + ME (1)
Ta có:
+) BG và ME cùng vuông góc với AC nên suy ra ME // BG hay ME // IG
Lại có: MF song song với AC hay MI // EG.
Suy ra MIGE là hình chữ nhật.
Do đó ME = IG (2)
+) Tam giác FBM cân tại F (do hai góc B và M bằng nhau). Với MD là khoảng cách từ M đến FB và BI là khoảng cách từ điểm B đến FM. Chứng minh tương tự Bài 9.8, ta dễ dàng suy ra được MD = BI (3)
Từ (1), (2), (3), (4) nên suy ra: MD + ME = BI + IG = BG = CH.
Vậy tổng khoảng cách từ M đến AB và AC chinh bằng khoảng cách từ C đến AB nên không đổi (đpcm).
Lời giải
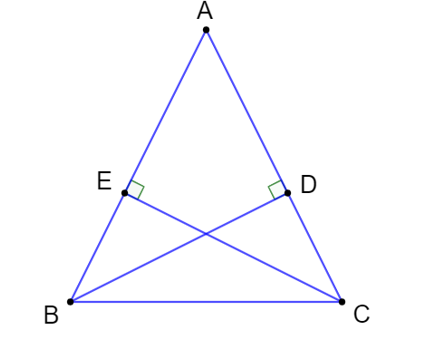
Kẻ BD ⏊ AC (D ∈ AC); CE ⏊AB (E ∈ AB).
Xét ∆ADB và ∆AEC có:
chung
AB = AC (Do ∆ABC cân tại A)
Do đó ∆ADB = ∆AEC (cạnh huyền – góc nhọn)
Suy ra BD = CE (hai cạnh tương ứng) (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.