Câu hỏi:

12/07/2024 1,160

a) Giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D nằm giữa A và C. Chứng minh AC > AB.

Câu hỏi trong đề: Giải SBT Toán 7 KNTT Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

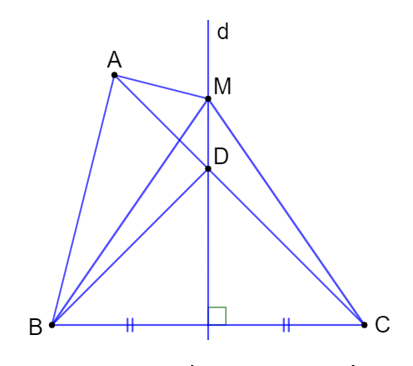
a) Giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D (ảnh 1)

a) Nếu đường trung trực d của cạnh BC cắt cạnh AC tại điểm D nằm giữa A và C thì ta có DB = DC (do D nằm trên đường trung trực của canh BC thì sẽ cách đều hai đầu mút).

Từ đó ta có: AC = AD + DC = AD + DB (1)

Trong tam giác ABD, theo bất đẳng thức tam giác, ta có: AD + DB > AB (2)

Vậy từ (1) và (2) ta suy ra được: AC > AB (đpcm).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh $\hat{B A C} = 45 °$ .

Xem đáp án

Lời giải

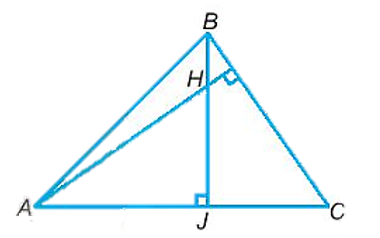
Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh góc BAC= 45 độ (ảnh 1)

Gọi BJ là đường cao xuất phát từ B của tam giác ABC.

Xét hai tam giác AHJ và tam giác BCJ có:

AH = BC (gt)

$\hat{A J H} = \hat{B J C} (= 90 °)$

$\hat{J A H} = \hat{J B C}$ (hai góc cùng phụ với $\hat{J B C}$ )

Do đó ∆AHJ = ∆BCJ (cạnh huyền – góc nhọn).

Suy ra AJ = BJ (hai cạnh tương ứng).

Xét tam giác JAB vuông tại J có AJ = BJ (cmt) nên JAB là tam giác vuông cân tại J.

Vậy $\hat{B A J} = \hat{B A C} = 45 °$ (đpcm).

Câu 2

Cho tam giác ABC vuông. Kẻ đường thẳng vuông góc với cạnh huyền BC của tam giác ABC tại điểm D không thuộc đoạn BC. Nó cắt đường thẳng chứa cạnh AB tại E và cắt đường thẳng chứa cạnh AC tại F. Xác định trực tâm của tam giác BEF.

Xem đáp án

Lời giải

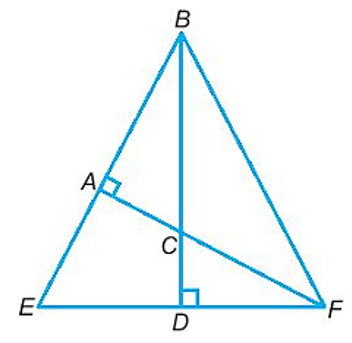
Cho tam giác ABC vuông. Kẻ đường thẳng vuông góc với cạnh huyền BC của tam giác ABC (ảnh 1)

Trong tam giác BEF, đường cao xuất phát từ B là đường thẳng BD, đường cao xuất phát từ F là đường thẳng FA.

Hai đường cao BD và FA cắt nhau tại C.

Vậy C là trực tâm của tam giác BEF.

Câu 3

Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S. Chứng minh tia PO là tia phân giác của góc RPS.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

b) Hỏi đảo lại có đúng không tức là nếu tam giác ABC có AC > AB thì đường trung trực d của cạnh BC có cắt AC tại điểm nằm giữa A và C không?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

c) Vẫn giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D nằm giữa A và C. Với M là một điểm tùy ý thuộc d, M khác D, hãy chứng minh MA + MB > DA + DB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

a) Giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D nằm giữa A và C. Chứng minh AC > AB.

Bình luận

Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh BAC^=45°.

b) Hỏi đảo lại có đúng không tức là nếu tam giác ABC có AC > AB thì đường trung trực d của cạnh BC có cắt AC tại điểm nằm giữa A và C không?

c) Vẫn giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D nằm giữa A và C. Với M là một điểm tùy ý thuộc d, M khác D, hãy chứng minh MA + MB > DA + DB.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh $\hat{B A C} = 45 °$ .