Cho hình bình hành ABCD, góc A < 90⁰. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. Chứng mình rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 2: Góc với đường tròn có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

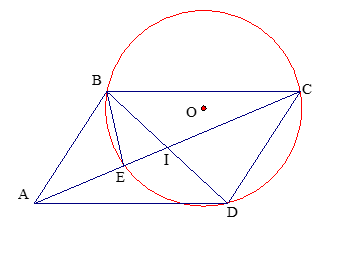
Cho hình bình hành ABCD, góc A < 900. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. (ảnh 1)

Gọi I là giao điểm hai đường chéo của hình bình hành.

IA = IC Þ $I E . I A = I E . I C$

$Δ I B E Δ I C D$ (g.g) Þ $I E . I C = I B . I D$

Từ đó suy ra: IE.IA = IE.IC = IB.ID = IB² . $\Rightarrow \frac{I B}{I E} = \frac{I A}{I B}$

Ta có ∆IBE và ∆IAB có $\frac{I B}{I E} = \frac{I A}{I B}$ và $\hat{BIA}$ chung , suy ra $Δ I B E Δ I A B$ (c.g.c) nên $\hat{I B E} = \hat{IAB}$ .

Suy ra BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB( định lí bổ sung)

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. Gọi I là giao điểm của AB và CD. Chứng minh rằng: $\frac{I C}{I D} = \frac{M C}{M D}$ .

Xem đáp án

Lời giải

Trình bày lời giải

Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. (ảnh 1)

Ta có $\hat{M A C} = \hat{A D C}$ (góc tạo bởi tiếp tuyến và dây cung); $\hat{AMD}$ chung. Suy ra $Δ M A C ∽ Δ M D A$ (g-g) suy ra: $M A^{2} = M C . M D$ và $\frac{M A}{M D} = \frac{A C}{A D}$

Tương tự: $Δ M B C ∽ Δ M D B$ suy ra: $\frac{M B}{M D} = \frac{B C}{B D}$

Xét $\frac{MC}{MD} = \frac{MC.MD}{{MD}^{2}} = \frac{{MA}^{2}}{{MD}^{2}} = \frac{MA}{MD} \cdot \frac{MB}{MD} = \frac{AC}{AD} \cdot \frac{BC}{BD} (1)$

Mặt khác : $Δ I A C ∽ Δ I D B$ suy ra: $\frac{I C}{I B} = \frac{A C}{B D}$

$Δ I B C ∽ Δ I D A$ suy ra: $\frac{I B}{I D} = \frac{B C}{A D}$ ;

Do đó: $\frac{AC}{AD} \cdot \frac{BC}{BD} = \frac{AC}{BD} \cdot \frac{BC}{AD} = \frac{IC}{IB} \cdot \frac{IB}{ID} = \frac{IC}{ID} (2)$

Từ (1) và (2) suy ra: $\frac{I C}{I D} = \frac{M C}{M D}$ .

Câu 2

Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. Kẻ tiếp tuyến AK với đường tròn (M, MB), K là tiếp điểm. Chứng minh rằng DK vuông góc với AM.

Xem đáp án

Lời giải

Trình bày lời giải:

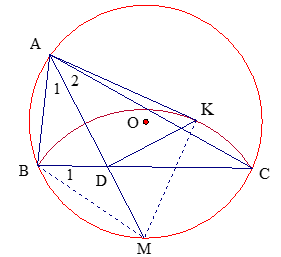
Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. (ảnh 1)

$\hat{A_{1}} = \hat{A_{2}}$ mà $\hat{B_{1}} = \hat{A_{2}}$ ( góc nội tiếp) nên $\hat{B_{1}} = \hat{A_{1}}$ .

$Δ M B D ∽ Δ M A B$ (g.g) $\Rightarrow \frac{M D}{M B} = \frac{M B}{M A} \Rightarrow \frac{M D}{M K} = \frac{M K}{M A}$

Kết hợp với $\hat{D M K} = \hat{A M K}$ (góc chung)

ta có: $Δ D M K Δ K M A$ (c.g.c) $\Rightarrow \hat{MDK} = \hat{MKA} = 90^{°}$

Vậy DK ^AM.

Câu 3